計算情報学２ 鈴木泰博

第4回

概要 第3回まではルール力学系を扱ってきた．第４回は非線形方程式の数値解法を扱う．通常は「数値計算」の講義のながれ（つまり数値解析としての扱い）であったが，このコースでは「ルールがある世界」として特徴づける．導入から，2分法，はさみうち法，ニュートン法までをあつかう．

注意:このコースでの演習の多くには，「唯一の模範回答」はないと思ってほしい．もっとも数学の演習問題は正答が存在するが．前回の演習，これから行ってもらう演習ともに，３０名の受講者がいれば，３０通りの回答があってよい（間違っていればハナシは別だが..）．

課題のすすめかた：今回の課題は１問づつNUCTにいって回答するとは違った方法をとる．

1. まず，テキストエディタ（WORD, メモ帳，emacs, vi, atom.. なんでもよい）をひらく

2. 課題1から順に回答していく．資料を順に読み進めていくと，課題が出てくるので，その回答を書き足していく

3. すべてが終わったら，NUCTから添付ファイルで提出する．

   ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

4. 締め切りは，原則として翌週の水曜日である（例外もある）．締め切りには注意する．締め切りを過ぎたら提出できない．９割以上の受講生の方々はきちんと，フォーマットも締め切りも守っている．

5. 締め切りが過ぎたら提出できない．課題はすべて評価しC以上であればカウントする．Fの場合にはカウントにならない．

   ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

ルールがある世界

ルール力学系では，自らがルールをつくってモデル化した．そこには，当然のごとく，あらかじめルールが存在していたわけではない．思う様にルールをこしらえて，うごかして，その様子をシミュレーションしてみたりしていた．これを数学的にどう表現するか？．．いろんな特徴づけはできるが，ひとつの言い方は「関数がない世界」である．

関数とは，世界，であり関数が決まるとその世界が確実に確定してしまう．$y = ax^2 + bx + c$と関数が与えられると，世界は２関数により規定される．そこには，原則として，不確実性はないし，すべて決定論的に規定されてしまう．この場合は世界は$x$と$y$の２次元である．$x$に値を代入すると，たちどころに$y$の値が得られる．逆に$y$の値を代入すると$x$の値を得ることができる．一般的にこちらのほうが難しい．たとえば，

$x^2 + 3x + 9 = y$

の場合に$x=1$を代入して$y$が14であることを求めることはとても簡単だ．だが，$y=0$の場合の$x$を求めることは，それにくらべるとずっと難しくなる．ちょっとやってみよう．

課題１　$x^2 + 3x + 9 = 0$となる$x$を求めよ．

課題１の世界を可視化しようとする．．と，世界が狭い，ことに気づく．数の世界は，深淵で，その底は見えない暗闇．映画「π」はその”暗闇”描いている．

もしそこに関数や方程式があるならば，私たちは蒙昧としたルール力学系の世界にいるのではない．自分で勝手につくるルール力学系の世界は，どことなしに不安だ（もしあなたが科学者ならば）．なにしろ，自分が勝手にこしらえたものだから，その実態は本当はよくわからない．５つの変数でルール力学系をつくれば世界は５次元だ．だが，それは自分のアタマがちょっと足りないだけで，本当は１変数で記述できるのかもしれない．そのモデルが重要なにかを指し示してる可能性があればあるほど，なんとか５変数が最適・最小の次元であることを祈りたくなるし，また，もしより最適・最小の次元があるなら，自分がそれをみつけて証明したいと強く願う．

だが，関数・方程式があるなら，ひとまずは安心だ．世界はそこに記述されている．その世界が正しいか，それとも自分がとんでもないヘマをしているのかと，冷や汗をかく必要はない．だがいざそれを「解こう」とすると，どうしょうもない困難，にぶつかることがある．たとえば先出のナビエストークス方程式については...いまのところ一般解はみつかっていない（ミレニアム懸賞問題のひとつ）．

方程式を解くのは難しくても，関数を解く，ことは「なんとかなる」．課題１についても，先人のつくった道具，を使うことで，なんとか解けたでしょ？でも，5次以上の高次関数になると．．あのような「便利な道具はない」（ことが300年ぐらい前に証明されている）．

そこをなんとかしよう！ということこででてくるのが，数値計算，なのである．やにわに数値計算のレシピに入るまえに，確認しておきたいことがある．これは長年，数値計算の講義を担当してきて，けっこう多くの学生さんが「ひっかかってしまう」ことだ．それは，

解って何？

ってことだ．「バカにすんな，あたりまえだろ」．うん，当たり前かもしれない，一般的に書くとたとえば解とは

$f(x) = 0$ をみたす $x$

となるだろう．では，これをグラフで図示してほしい．

課題２ $f(x)=0$ の解をグラフとして図示せよ

もちろん$f(x)$はさまざまに考えられる，１次関数だけではなく高次関数や特殊関数($e^x$や$log(x)$など）またその組み合わせなど，いろんな関数を想定すること．

この「あたりまえのこと」を，しっかりと心に刻まないと．．．迷路にはまっていくことになる．例年，最終試験で何時間も粘った挙句，うつむきながら白紙に近い答案を提出して背中を丸めて去っていく人々がいる．彼らは総じてこの「あたりまえに思えること」を，本当には理解していない（ことを，そんな彼らが必死で向き合った答案が示しているのだ）．

なんか"ヨビノリ"のようなノリになってしまうが...

「非線形方程式の数理解法はね「解とは幾何学的になにかをイメージすること！」これがポイントだからね！」

これから勉強する方法は，ゴルフのパターみたいな，イメージである．パターでは，曲面の変化．を読んで利用してゴルフボールをカップインさせる．数値計算では「曲面の変化」を方程式・関数が与えてくれる．これをうまくつかうと，早く，カップイン．．つまり$f(x)=0$となる$x$をみつけることができるわけだ．

”ルールがある世界”とはつまり，”ゴルフボールがどのように動くか”，原理的にはまったく未知ではなく，グリーン上の凹凸として与えられている，一方で，ルール力学系の場合には，いわば”グリーンの凹凸（方程式・関数）”がまったくわからない状態で... シミュレーションをたくさんやって，グリーンの凹凸を逆に推定するようなことをするわけっだ．

なので非線形方程式の数値解法とは「$f(x)=0$となる$x$を，いかに効率よく方程式・関数が規定する世界の凹凸をつかって求めるか」なのである．その方法は様々である．コンピュータがない時代にも技術者はもちろんいたわけで...現代土木工学でも造れないといわれている（本当に？）ピラミッドだって技術者がいろんな計算をして，高層建築をしていたのだろう...そうした先人たちの知恵のかたまりのようなものになっている（ひとは不便なほうが，賢くなるのかいな．．と思ってみたりしゅる..閑話休題）．

このコースで扱うのは，まずは３種類，

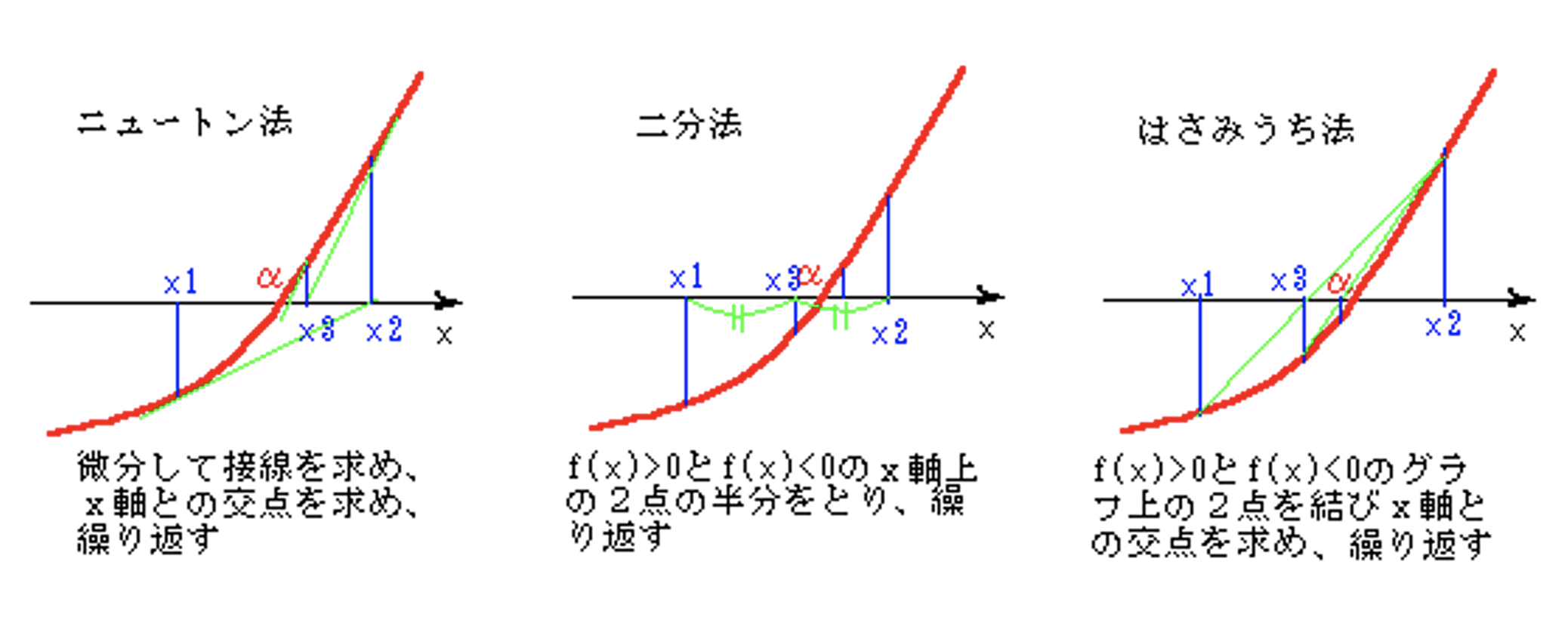
関数・方程式のもつ情報の活用度が低いものから，高いものに並べ替えると「二分法，はさみうち法，そしてニュートン法」の順となる．二分法はとても単純な方法だが，関数の情報（グリーンの凹凸）は，ほとんど使わない．なので，解を得るまでに時間がかかる．一方でニュートン法は，バリバリ関数の情報を使う．”ニュートン法”という名前から想像がつくかもしれないが．．．そう，微分〜つまり「傾き」をつかっちゃうのだ．

では２分法からはじめよう．２分法とはつまり「中間値の定理」である．実はですね，．中間値の定理の証明（区間収縮法）がそのまんま２分法なのでR．知っているひとは復習，初見のひとも，そんな難しいはなしじゃないので．．．

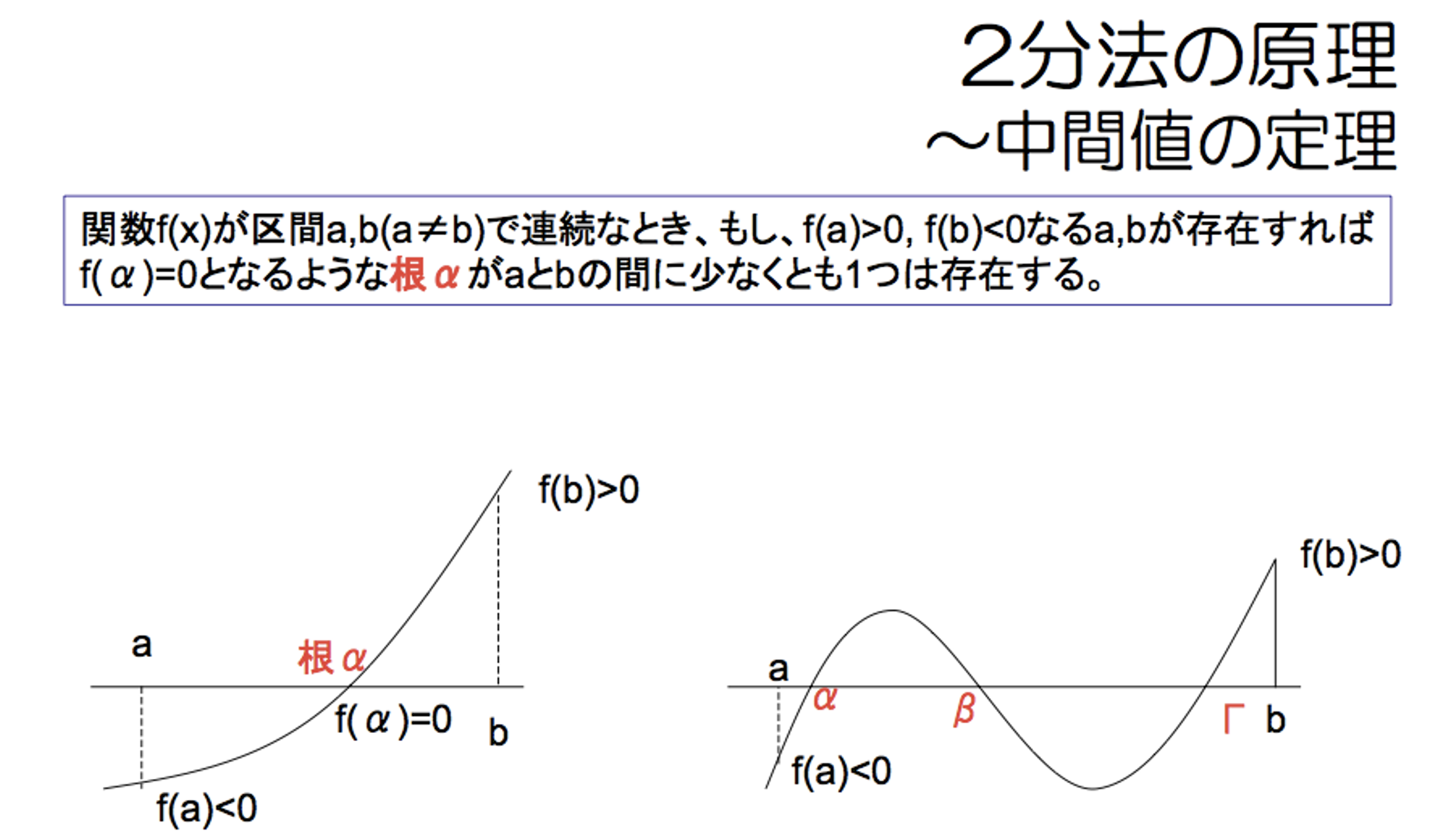
中間値の定理とは，とんでもなく大きい滑らかな布の，下から上に「１本の糸」を通す，場合に，布にまったく触れずには「糸」を通すことができない．糸が下から上に通った，ということは，どっかで布を突き破っているはずだ．それが，ものすごくざっくり言った場合の「中間値の定理」だ．

これは何を教えてくれるか？というと．．

ある区間$a, b$で関数・方程式の値の「符号が反転していれば」解はかならず区間$a,b$のなかにある

ことを教えてくれる．ほら，関数の傾きとかそーゆー情報はつかっていないでしょ．ここで使っているのは「解」はここにありますか？ありませんか？という情報を教えてくれる．

もし他の区間$b, c$をとったときに，$f(b)$と$f(c)$の符号が同じだったら．．どうなる？そこには解（布を突き通す糸）は...ない．ことを関数・方程式が教えてくれる．ならば，$a, b$の区間の幅を小さくしていけば，いくらでも解に近づけることができる（滑らかで，連続である条件が満たされていれば）．

だったら．．．$\frac{(a + b)}{2} = c$ として「区間を２分しましょう」というのが，その名のとおり「２分法」だ．

さて，いま区間を２分したわけだが．．．解は区間$a,c$と$c, b$のどちらに入っているのだろう？ここで中間値の定理をつかえばいいわけで，もし$f(a) < 0, f(c) > 0$ならば，符号が反転しているので，解は区間$a,c$にあることになる．これで区間は以前の半分になった．あとは$b=c$として，この操作を繰り返していけば，解にいくらでも近くことができる．もっとも無限回やっているわけにもいかないので，適当なところで打ち切ることになるが，その場合の区間$a,b$の長さが「精度」になる．

では，これをアルゴリズムでかいてみよう．

課題２：$f(x)=x^2-1$の解を２分法で求めよ．解は見ただけでわかるような例なので，解をレポートに書いても意味がない．やることは，

1. 初期値を定める；つまり，解が存在する区間$a, b$をとる．
2. 2ステップぐらい”手計算してみる”．
3. プログラムを書いて動かす．プログラミング言語は問わない．

はさみうち法

２分法は「解がこの区間にあるか？」だけの情報を方程式・関数から得ていた．プログラムも極めて単純なアルゴリズムで，「ゴルフのパターでのグリーン上の凹凸」に相当する情報は使っていない．「もう少し，関数・方程式の情報を使えないか？」という”工夫”こっからさきの話である．

2分法では，ただ区間を2分するだけだった．ここを工夫して２分ではなくて，より解に近づけるように区間を分割しよう．というのが”はさみうち法”である．で，どうやるか？

1. まず区間$a,b$をきめる
2. $a$と$b$を通る直線 $l$ を描く
3. 直線 $l$ が $x$ 軸と交わる点（つまり $l(x) = 0$の点なので，もっというと，これが解の候補ね）を，（２分法での）$c$ とする．
4. 2分法と同じように次の区間を決めて，2.に戻る．

課題3:

1)

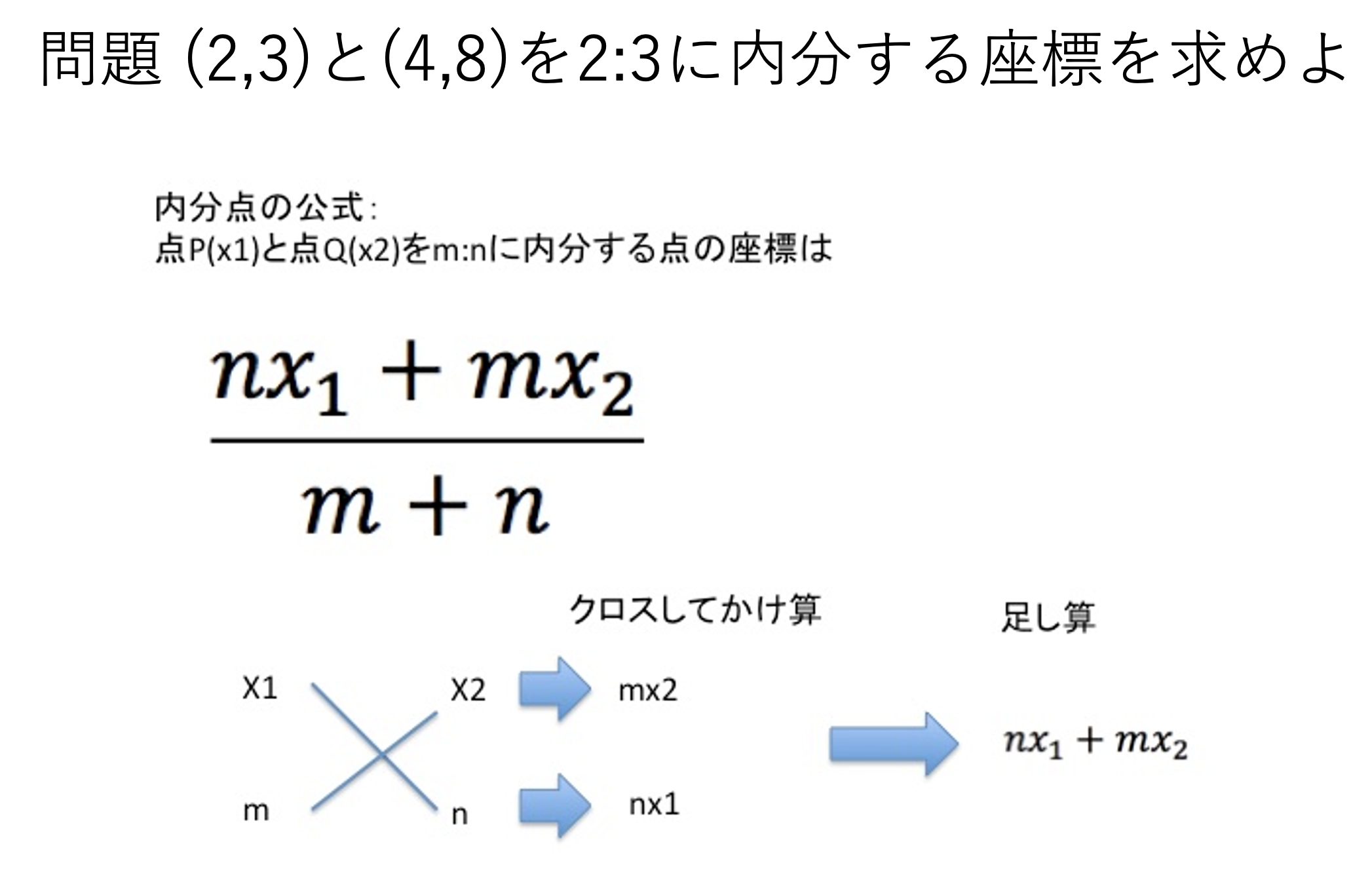
2)

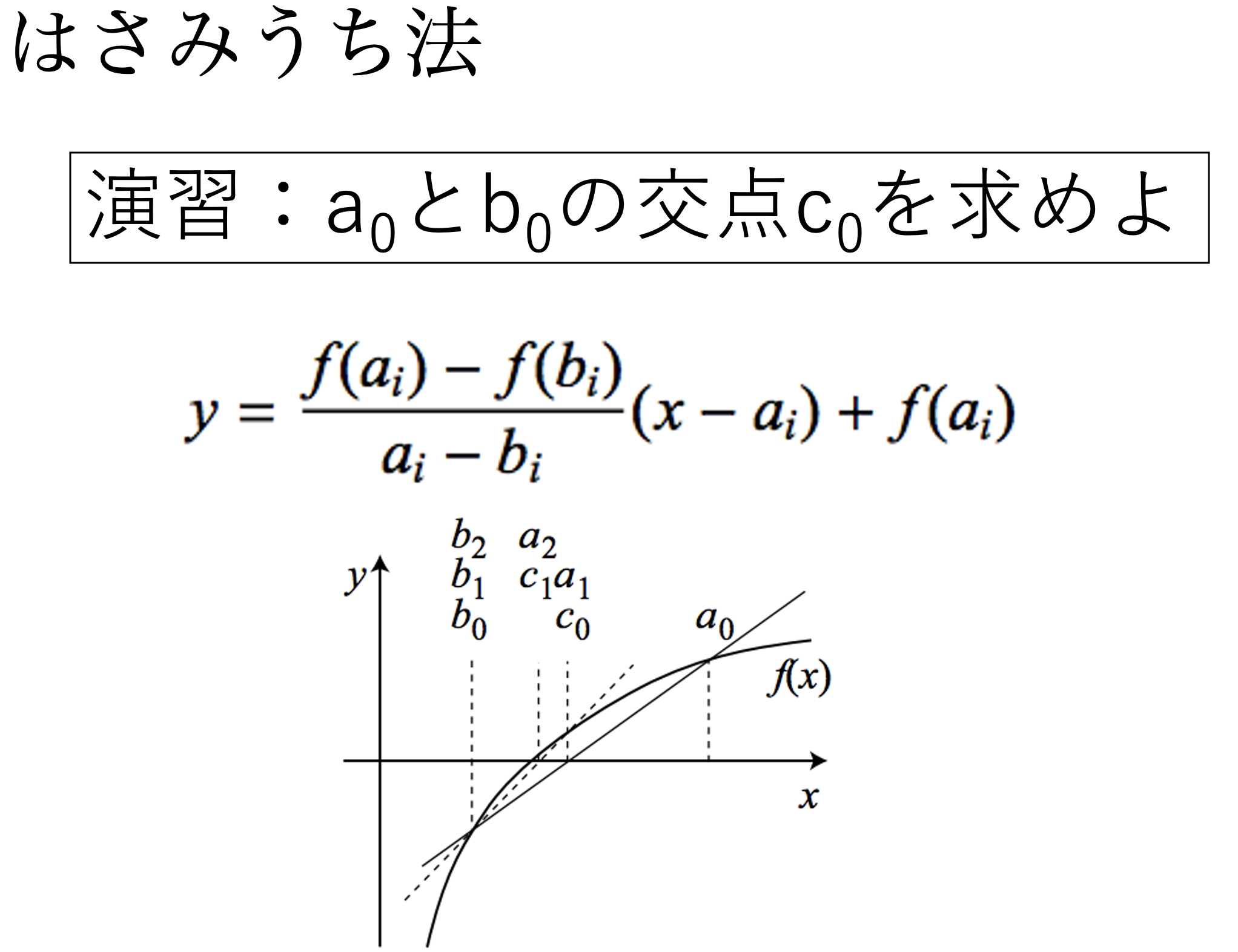
3) ?の部分を埋めて，文章を完成させなさい．

1)と2)より，はさみうち法とは区間(a, b)を(?):(?)に内分していることになる．

課題4：$f(x)=x^2-1$の解をはさみうち法で求めよ．解は見ただけでわかるような例なので，解をレポートに書いても意味がない．やることは，

1. 初期値を定める；つまり，解が存在する区間$a, b$をとる．
2. 2ステップぐらい”手計算してみる”．
3. プログラムを書いて動かす．プログラミング言語は問わない．

ニュートン法

さらに積極的に関数・方程式の情報をつかうのがニュートン法です．こちらは，ほとんど「ゴルフのパター」のように凹凸の情報をフルにつかって解をもとめていきます．

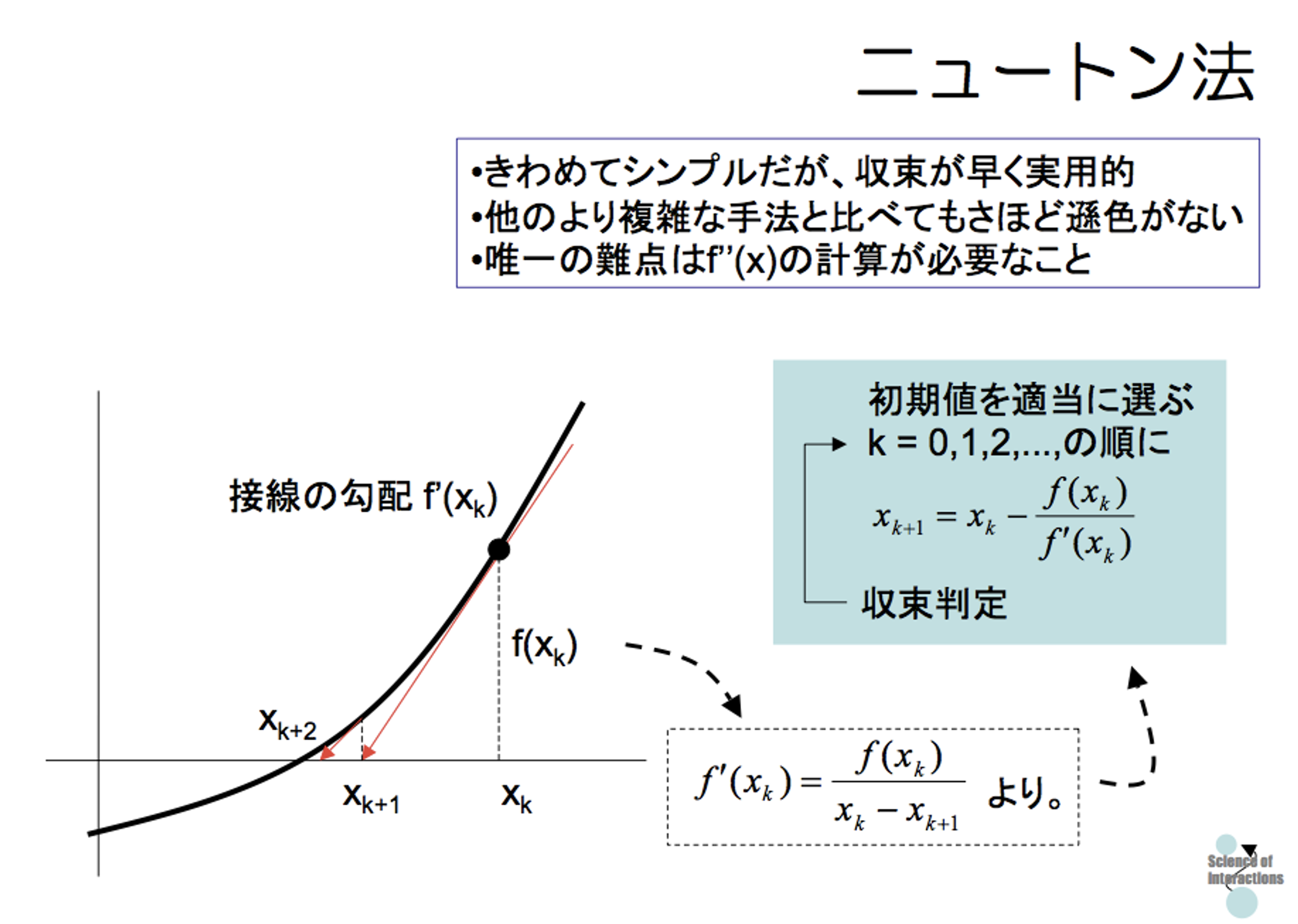
ニュートン法は初期値の $x$ での$f(x)$の傾きをつかって，次の点（これはさきほどまで$c$とされていた点）へ移動していきます．ニュートン法はいままでとちがって区間$a, b$からはじまるのではないので，初期値を$x_k$とします．$x_k$のつぎが$x_{k+1}, x_{k+2}, ...$と解にむかってすすんでいきます．

上の例では，まず$x_k$からはじまって，$f(x_k)$の傾きをもとめ，その傾きをつかって$x_{k+1}$をもとめます．そして$x_{k+1}$での傾きをつかって$x_{k+2}$をもとめ．．これを繰り返していきます．こうやってみると，関数・方程式の情報をフルにつかっていることがわかるとおもいます．

で，具体的にどうするのか？

導出はカンタンです．なぜなら，微分の定義そのままだからです．$x_k, x_{k+1}, x_{k+2},...$の記法をつかって微分を定義すると，上図にある

$f^{\prime}(x)=\frac{f(x_k)}{x_k - x_{k+1}}$

となります．

課題5:

1) 上述の微分の定義を式変形して$x_{k+1}=...$のかたちとせよ．

2) $f(x)=x^2-1$の解をニュートン法で求めよ．解は見ただけでわかるような例なので，解をレポートに書いても意味がない．やりかたは上述とおなじで，

• まず手で数ステップ動かしてみる
• プログラムを書いて動かしてみる

今回はここまでです．

おつかれさまでした．