計算情報学2 鈴木泰博
第6回
概要 前回は補間のなかでもいちばん簡単な「線形補間」を紹介した.今回は2次関数,高次関数による補間を紹介する.そして,そのながれで数値積分に入る.
注意:このコースでの演習の多くには,「唯一の模範回答」はないと思ってほしい.もっとも数学の演習問題は正答が存在するが.前回の演習,これから行ってもらう演習ともに,30名の受講者がいれば,30通りの回答があってよい(間違っていればハナシは別だが..).
課題のすすめかた:今回の課題は1問づつNUCTにいって回答するとは違った方法をとる.
まず,テキストエディタ(WORD, メモ帳,emacs, vi, atom.. なんでもよい)をひらく
課題1から順に回答していく.資料を順に読み進めていくと,課題が出てくるので,その回答を書き足していく
すべてが終わったら,NUCTから添付ファイルで提出する.
********************************************
締め切りは,原則として翌週の水曜日である(例外もある).締め切りには注意する.締め切りを過ぎたら提出できない.9割以上の受講生の方々はきちんと,フォーマットも締め切りも守っている.
締め切りが過ぎたら提出できない.課題はすべて評価しC以上であればカウントする.Fの場合にはカウントにならない.
********************************************
補間
前回は直線,つまり1次関数による補間を行なってみた.1次関数だと「曲げる」ことができないために,以下のように,各ポイントが「曲がって」いると,線のひきようにない.
「さて..どうするか?」
「ならば,補間多項式を”曲げて”しまえばいい」
たとえば,2次関数にすれば「1回曲げることができる」.この場合は1回曲げれば,すべての点を通る補間多項式ができる.ならば,
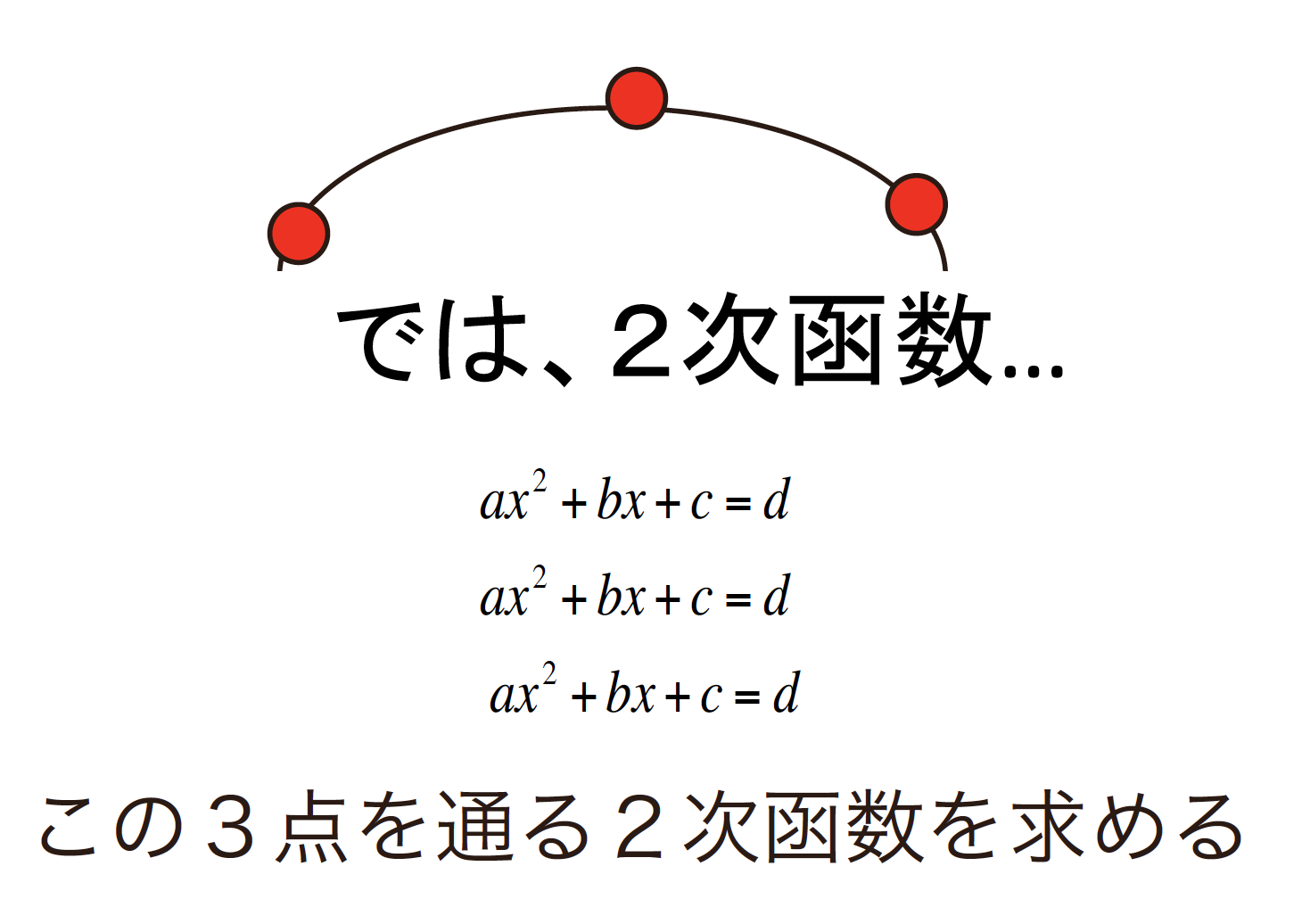
3点を通る2次関数を求めるためには,以上の連立2次方程式を解けばいい.ここではあたえられているので,未知数は3つだ.やってみよう.
課題1: 3点を通る2次関数は以下のようになった.この連立方程式から補間多項式(3点を通る関数)をもとめよ.
この方法を使えば,n次方程式をつかえば,どんどん曲げてn+1点を通る関数を求めることができる.だがそのためには,n次方程式を解かねばならないわけだが.というわけで,次のチャレンジ課題(計算力に自信があるひとはやってみてください).
チャレンジ課題:の3点を通る2次関数を求めなさい.
ヒント:
の3点を通る二次関数
の3点を通る二次関数
の3点を通る二次関数
についてとおきます.ここにを代入するとどうなりますか?
このチャレンジ課題をといてみると,ちょっと複雑な式がもとまります.この式は「ラグランジュ補間多項式」とよばれるものです.

課題2:上図での「演習」を行いなさい.
課題2を行なってみると(チャレンジ課題ができたひとはより深く理解できたでしょう),この補間多項式が複雑そうにみえて,実によくできていることがわかるでしょう..か?
「どこが,よくできているの?」
この式の形からして,をいくらでも増やしていけそうですよね?
課題3:m=4の場合のラグランジュ補間多項式を求めなさい.
課題3でわかるとおり,m=5,6,..といくらでも増やしていけるわけです.もっと具体的な問題で「慣れましょう」.

課題4:上図の演習を行いなさい.
「課題4がうまくできているか不安です.答えを教えていただけませんか?」
との質問が来る前に,お答えします.
「求められた補間多項式が,合っているか,間違えているかは,実際にを代入しての値と合っているかどうかをたしかめればOKです!
数値積分
補間多項式から数値積分だなんて..えらくジャンプするかんじがしますが..実は,補間多項式からの流れで数値積分になってしまうのです.
まず,簡単な定積分を計算してください.
課題4
をもとめなさい
きわめて簡単な定積分ですが,手で計算しているときには解析的な性質を全部前提にして,計算をしています.それと同じことを計算機にやらせよう,しかも任意の関数に対して定積分をやらせようとすると計算は連続や無限が扱えないので..同じことをさせることはできません.
そこで,連続・無限の世界から,離散・有限に世界に移ります.そこで,出てくるのが高校時代に勉強した区分求積です.区分求積は大きく分けて2つ,右端と左端があります.が矩形の右上を通るのか,左上を通るのかの違いです.やってみましょう.
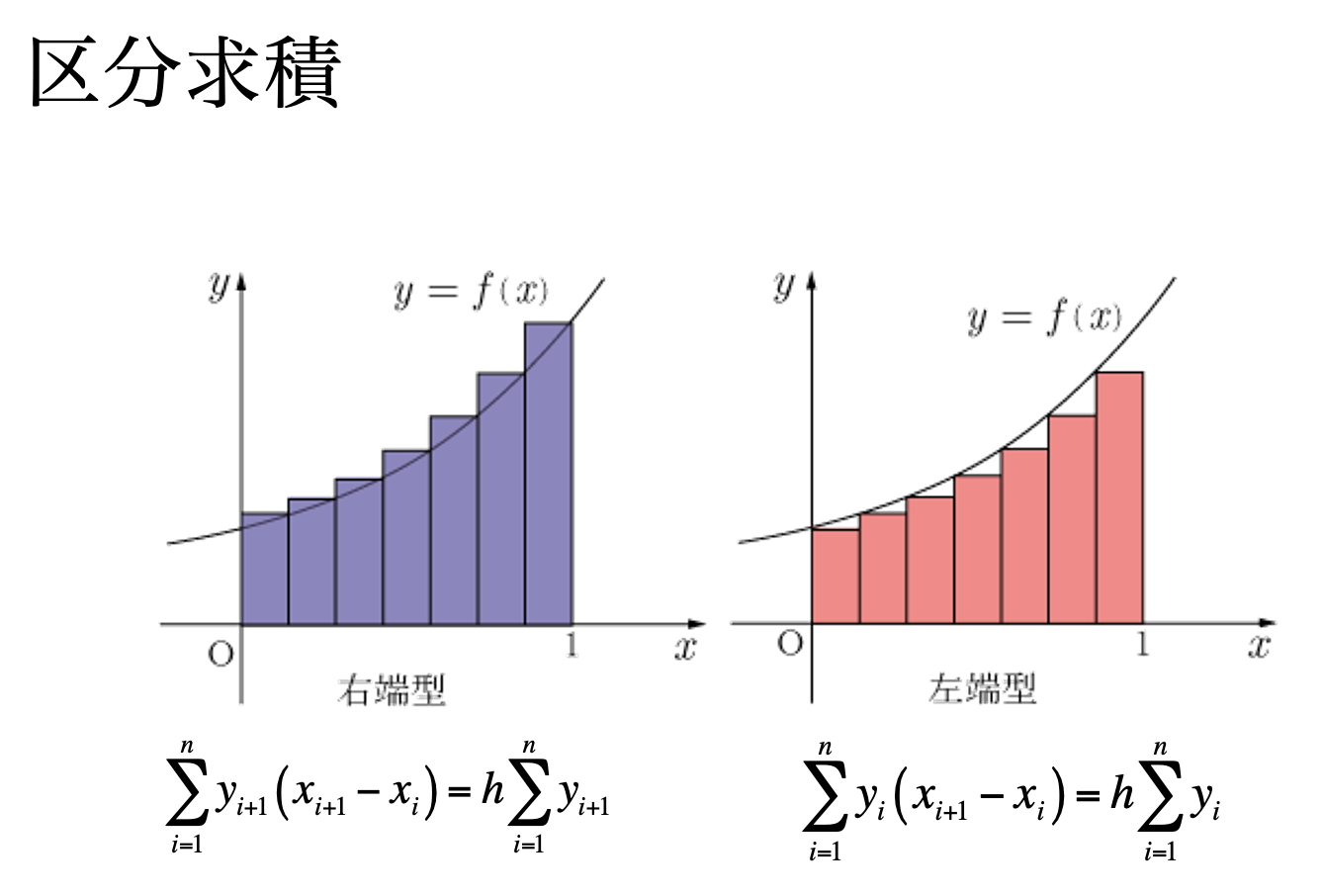
課題5
1) を右端区分求積と左端区分求積で求め,解析解と比較しなさい.
2) 1)による比較より,この区分求積法は誤差が大きくなることがわかります.その誤差を小さくする区分求積法を考案して,計算してみて,解析解と比較しなさい.
余談.
人工生命,複雑系,複雑ネットワーク,シンギュラリティ,..ずいぶんといろんな概念が流行してきたもんである.日本でもシンギュラリティはもう流行が過ぎたかんじであるが,カーツワイルがこの概念を分厚い本,singurality is nearにまとめたのは,日本で流行する10年ぐらい前だった.
最近は,コンセプト自体をぶちあげる式,の動きがめっきりと亡くなった気がする
人工生命や複雑系が隆盛の頃は,祭り,の状態で,いろんな概念が出され,そもそも分野全体に「なにかが起こるかもしれない予感と興奮」みたいなものが渦巻いていた.まだ,学生か助手(現在の助教)になりたてのころに第一回の複雑系の国際会議がボストン片田舎で行われた.当時にうれていた科学者やノーベル賞科学者が複数参加した会議で,会場は熱気に包まれていた.英語もよくわからんけど,「現場の熱」,みたいなものを肌で感じることができたのは貴重な経験だったと思う.
それに似た興奮は,ヒトゲノムが公開された直後にもあった.ヒトゲノムはいまでは「なんでもない」はなしだけど,当時のバイオインフォマティクスの現場では,驚愕だった.当時は短い配列を決めることしかできず,ヒトのような長大なゲノムが読めるようになるのは「ずいぶん先」と思われていた.
そこに,クレイジーな考え+ITの力技,でガンガン解いていく方法(ショットガンメソッド)がでてきたときには,大いに驚いた.どっかで..あれはどこで聞いたんだっけかなぁ..グレグ・ベンターが講演で「グラントを申請して,ヒアリングに呼ばれたが,ヒアリングの前に申請していた動物種の全長ゲノムを決めていた」といっていた.「すげーな」とおもったもんだ.
でも,そのあとで,そもそもDNAのシーケンシングの技術の基礎は日本人がつくったこと.当時の役所がその特許性をみとめずに棚晒しにしてしまったこと,日本のシーケンシングの技術の高度さに恐れをなした米国が(自動車で日本に負けた直後)巻き返しを行い,知財もみな米国にもっていかれてしまったこと..をその黎明期の技術をつくられた先生とその関係者から聞いて..暗澹たる気持ちに沈んだ.
「日本は日本人を決して認めない」
これを強く打ち込まれた.助手の頃に燦然と輝いていた,cDNAのライブラリー研究を世界的にリードしていたさる先生は,当時の政権与党の「2番じゃだめなんですか」攻撃にあって,予算をズタズタにされ,米国へと移り,日本からガンの免疫療法の研究がほぼ完全に消えてしまったり...
こうした状況は,いまでもあんま変わってない気がする.
閑話休題.
さて,アイデアでました?右端と左端よりもよい求積法は見つかりましたか?では,まずいっぱつめ,

課題6:上の演習を行なってください.
ここまでは,思いつくひとも多いでしょう.
では,次はどうでしょ?
これは,結構な「発想の転換」が必要になります.矩形というイメージから,いったん,抜けて頭を柔らかくしてみると,「あっ!」と気づく方法です.
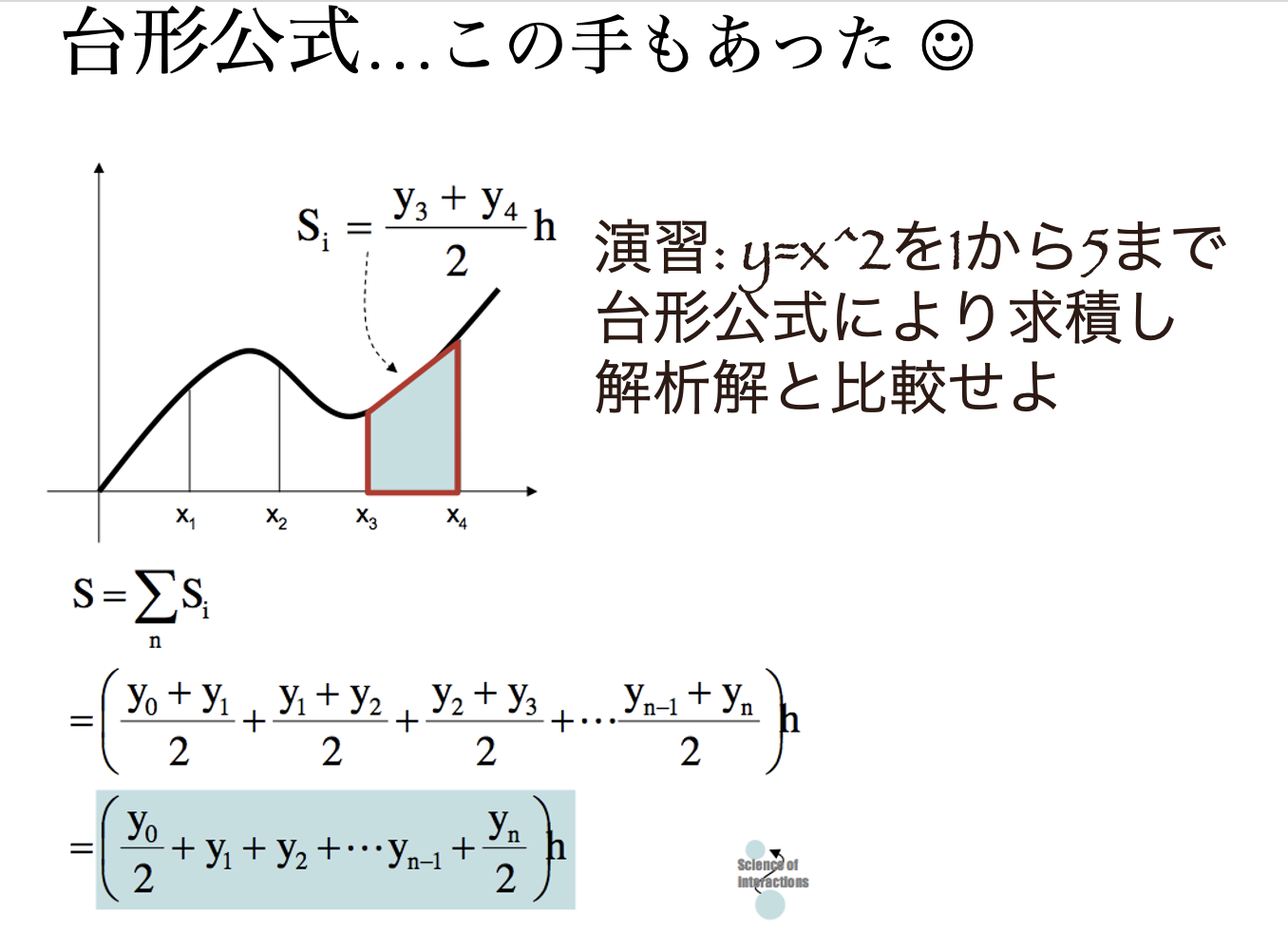
課題7:上の演習をおこなってください
これで終わりでしょうか?
まだ頑張れば,考えられそうですよね.
この先,どんな手をつかいますか?これまでの流れから想像がつくのは..なんですか?
いままで線形で近似をしてきました.補間のときと同じですね...とすると,次の1手としてかんがえられるのは,そうです2次関数で近似する方法です.
2次関数で近似するので..積分区間のうち「3点分」は2次関数で近似をすることができます.なので,3点分だけラグランジュ補間(m=3)をして,そのラグランジュ補間多項式そのものを積分しちゃうという方法です.そして3点をずらしていきます.
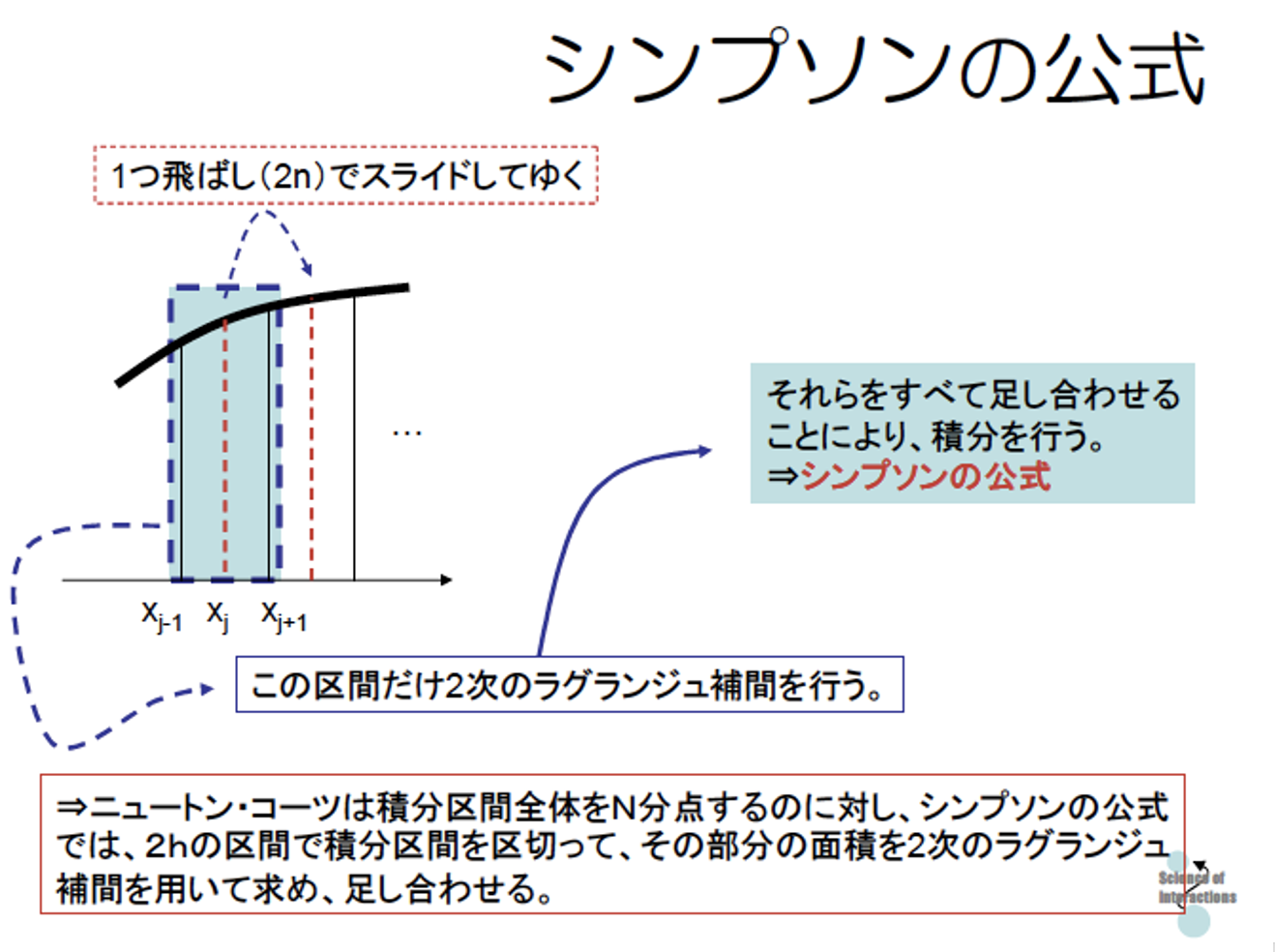
さて,具体的にどうなるか?計算力があるひとは,チャレンジしてみてください.次回はシンプソンの公式からはいって,微分方程式の数値解法へとすすんでいきます.
今回はここまでです.
課題をNUCTから提出してください.締め切りに注意!
おつかれさまでした.