計算情報学2 鈴木泰博
第8回
概要 微分方程式,偏微分方程式などの,いわゆる数値解析は「計算情報学1」の講義で扱うので,最終回である今回は,このコースの前半に行った離散時間・離散事象の確率過程モデルと,前回にみなさんが,手を動かして勉強したオイラー法との関係に触れて終わることにする.
注意:このコースでの演習の多くには,「唯一の模範回答」はないと思ってほしい.もっとも数学の演習問題は正答が存在するが.前回の演習,これから行ってもらう演習ともに,30名の受講者がいれば,30通りの回答があってよい(間違っていればハナシは別だが..).
課題のすすめかた:今回の課題は1問づつNUCTにいって回答するとは違った方法をとる.
まず,テキストエディタ(WORD, メモ帳,emacs, vi, atom.. なんでもよい)をひらく
課題1から順に回答していく.資料を順に読み進めていくと,課題が出てくるので,その回答を書き足していく
すべてが終わったら,NUCTから添付ファイルで提出する.
********************************************
締め切りは,原則として翌週の水曜日である(例外もある).締め切りには注意する.締め切りを過ぎたら提出できない.9割以上の受講生の方々はきちんと,フォーマットも締め切りも守っている.
締め切りが過ぎたら提出できない.課題はすべて評価しC以上であればカウントする.Fの場合にはカウントにならない.
********************************************
このコースの「道のり」を再度振り返ってみよう.このコースでのテーマは「力学系」だった.力学系とはなにか?まだ覚えているだろうか?
ざっくりいって「時間とともに,状態が変化する系」
が力学系だったですね.
そして,最初は「おはじき」をつかうような,ひじょうーに簡単なモデルをつくってみて,コインを投げたりしながら,しみゅれーしょん,をしてみたりした.おもむろにコインやサイコロを投げていた頃を思い出して欲しい.
「そこに,関数はありましたか?」
「いいえ,ありません」
「関数がない?では,あなたはどんな”世界”にいたのですか?」
「さぁ..わかりません」
そうなんです.コインやサイコロ投げてシミュレーションしちゃってるってのは,「自分がどっこにいるのか,さっっぱりわからんちん」だからなわけ.もし,わかってんだったら,コインやサイコロ投げずに,ノートに
と書いておしまい.あとは初期値さえきまれば,すごく大雑把な言い方ではあるが,月にだって行ける.関数がない世界とは”無政府状態”みたいなものなので,ルール力学系として
と定義されていても,「そこにがあろうとも, しか適用できないのでつ!」と,の数をひたすらに,指数的に爆発させていったとしても..まぁいいわけです.あとは,これは「生命の起源のモデルだ」とか,「生態系のモデルになっていて..」と言って押し通してしまうわけですね(私がかつて行っていた研究はこんなかんじ).
これはこれでよい.楽しいし.
でも,この無政府状態みたいな世界にいると,厳しくも美しい秩序がある数学の世界や,合理的な手法の宝庫である物理学の世界と,まず繋がることができないわけです.なんか,ポツん..といるかんじ.自分の世界を数物の世界から見返すなんてことができないので「自分がやっていることって,この世界から出るとどうなってんだろう?」ということも,わからんちん. 実験をやっているとか,フィールドワークをやっているとか(まぁフィールドワークもなかなか,情報量を落とすのが難しくて独我的になっちゃうんだけどね),なんか,自分の世界とリアル,が結びついていたらいいんだけど..
無政府状態のルール力学系の世界に,少しでも秩序を入れるための「法」それが...何でしたっけ?
ルールの適用方法
これが「法」.このコースで扱ったのは2つ,
- 逐次+ランダム(コインやサイコロ):つまり「非決定的」
- 可能な限り並列(maximally parallel):つまり「決定的」
であった.決定的を「決定論的」を書いていた気がします..すいません.英語だと,non-deterministicとdeterministicにになります.
ルール力学系を「離散・有限」で並列にするにはムリがあった.そこで,連続・無限に拡張をしたわけだ.ここがいささか「乱暴」なところだった.オイラー法を前回にやって準備ができたので,少しばかり,このあたりを補足しておわることしよう.
「離散・有限」系から「連続・無限」系への変換
つかうルール力学系は,以前に例題につかった {}とする.うさぎとキツネのモデルだ.まず「離散・有限」系(非決定的)からはじめるて,それを「連続・無限」の系(決定的)にしていくだけだが,これをしっかりやるとすると,いろいろ大変なので,天下り的に以下を認めて欲しい
「ルール力学系の適用確率は,ルールの左辺の積に比例する.比例定数をそれぞれとする.」
これはなにかといえば... 適用確率をランダムにするのではなく,重みをつける,ということだ.完全ににランダムだとと3つ目があるサイコロを振ることになるが,そのサイコロを”いかさまサイコロ”にするわけだ.しかも,いかさま,の度合いが時間とともに変化してしまうような,サイコロだ.
この場合は確率が時間とともに変化するでしょ.こういった方程式を「確率微分方程式」といいます.
「え,なんか急に出てきたな.なんでまた確率微分方程式なんですか?」
「変位の時間変化は?」
「速度です」
「どうやって求める?」
「そりゃ,変位を微分すりゃいいんです」
「えっと,も一度聞くけど..速度ってなんだっけ?」
「変位の時間変化です.だって微分するんだからっ!」
「じゃあ,確率の時間変化は?」
「あれ,,確率微分...になっちゃいますね..」
たとえばはウサギの羽数なので,の適用確率は,ウサギの羽数にをかけたものになる.同様にはとなる(r_3$は類推できるでしょ).
すると各々のルールの適用確率は,
となる.
つぎに, は記号のままだと扱いにくいので,ベクトルにしてしまおう.ではが1つ増えるので=(1, 0)とする.以下この要領でいくと,となる.
これで,いかさまサイコロ,をつかって「うさぎとキツネ」のモデルを数理モデル化することができた.
ここまでは,離散・有限の系である.さて,ここからこの系を「連続・無限」の系へと変化する!といってもね,そんなタイソーなもんじゃなくて,中高の算数で十分.
この系は「非決定系」なので,これを,決定系にしたい.誰でもおもいつく方法は?
「え,平均とればいいんじゃないの?」
「はい,その通り」
「確率の場合の平均ってなんでしたっけ?」
「期待値!」
「其の通り」
というわけで,期待値をとってしまえば,決定論系になって連続・無限系になってしまうのである.あら簡単.
はい.これで,期待値が求まりました...つまり,「もう確率系じゃありません」それに,離散でもありません.だって有理数(分数)を掛けてますからね.
これで,めでたく,離散・有限の数理モデルを,連続・無限の数理モデルに変換することができました.得られた方程式は,
となります.
ここで とすると,
となります.
この連立方程式は,どっこにも「乱数」がありませんっ!.これが私がたちがもとめていた関数..方程式なのです!
「わーい!これで,エクセルでも計算できる!」
....ってわけには,ちゃんとやるとすると,いかないんですよ.だっては変化してしまいますから,これは定数ではないのです.あらら..でも,がっかりする必要はありません.私たちは,無限の世界に移住してきたので「は無限」といったってよいわけです.まぁ,うさぎやキツネが無限にいるというのも,あまりリアリスティックじゃないので,「十分にたくさんいる」,とかゆってもOKなわけです.
「で,どのぐらいたくさんいるの?」
ここで,この質問になんと答えるかが大変に重要です.ここでは,おもむろに,
「少々変動しても,の値の変動がよりも小さいぐらいに,たくさんいる」
と答えるのです.そしてこう付け加えます,
「そして,は十分に小さいとします」
つまり...分母が100,000のときにが1,2ぐらい動いたっての変化は程度でしかありません(). 一方で分母が5のときには,が1動いたっては大きく変化してしまいます.わたしたちは無限の世界にいるので,いくらでもは大盤振る舞いができるので,が十分におおきく時間 内ではその変化は無視できるので定数とする.としてしまえば,この方程式はさらにシンプルになって,
となります.ずいぶん,すっきりした方程式が得られました.これで,もう簡単に計算できますね.
課題1 上の方程式のシミュレーションを行いなさい.係数や初期値はいろいろ試してみてください.
ヒント:この方程式は.簡単に振動します.なので,振動させてみてください.実際には初期ベクトル,=(うさぎの羽数, キツネの頭数)にを足していくことになります.
つまりとなるわけね..
口調の揺れが激しいが..気にせずに先へすすむとしよう.
さて,私たちは非決定系から決定系を得ることができた.なぜうまくいったのか?それは無法状態だったルール力学系の世界で「法」を定めたからだった.それによって,方程式が浮かび上がってきた.これまでは,離散・有限の世界にいて,えっちらおっちらと,連続・無限の世界に渡ってきたのだが,最初っから,連続・無限の世界にいたらどうなるのだろう?「もし,私たちが決定系の世界の住人だったら?」
モデルは同じ「うさぎとキツネ」であって,
である.さて,これを決定系で数理モデル化するとどうなるか?2変数だから連立微分方程式になるわけで...どう考えるかというと,以前に練習したけど「増減のしかた」を調べればよろしい.の変化はどうなってますか?で増えて,で減るから,
となるね.同様にしては
となるね.これで,あっという間に決定論の数理モデルが得られた.
課題2 この連立微分方程式をオイラー法でシミュレーションせよ.係数は初期値は任意.
長いヒント:この方程式は,容易に振動する.なので,振動させてみてほしい.まず,オイラー法の復習をすると...
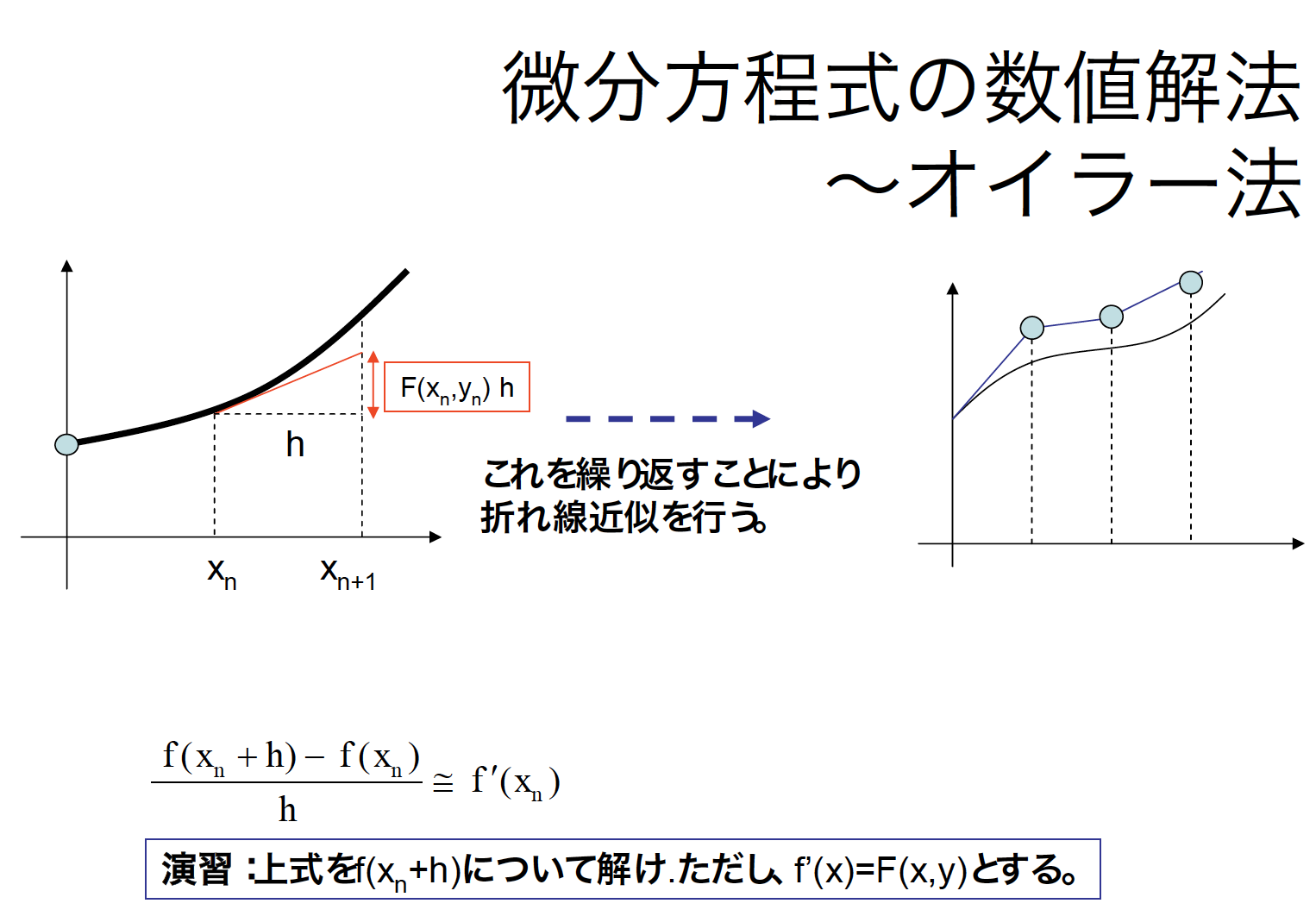
課題2の場合は
となるわけで,, となる...と.あとは,オイラー法のスキームに放り込んでおしまい..っと.
まずについてはとなって, についてはとなるわけね...ここまで,書き下してくると,さすがに気がつくでしょ? ひきつづき課題2をやってください.
課題2が終わって...
さて,「なぜこうなったか」わかりますか?
連続・無限の世界で「オイラー法」をつかうってことの意味は...まず,時間をとかいって離散的に「切り刻む」こと,すると連続だった区間が初期値と「点列」になって離散化されて,しかも計算を永遠に行うわけでなくて有限時間で止めるので,有限個の点列になってしまうわけです.
つまり,オイラー法をやってしまう...ということは,本来は連続・無限であった世界から離れて,離散・有限の世界へと向かうことなのです.この方向にずんんずんと進んでいくと,離散・有限の世界からえっちらおっちらとやってくる,先ほどの私たち,と出会ってしまうわけですね.
ルール力学系を適当にでっち上げて,ルールの適用をmaximally parallerにすれば微分方程式(系)だよん〜って,ゆってたわけですが,その「たねと仕掛け」はこんなかんじです.計算情報学1を履修するひとは,重複するので触れなかったルンゲクッタ法を学ぶと思いますが...もちろん!以上の確率過程系でルンゲクッタを用いることもできます.
今回はここまでです.
締め切りに注意してNUCTから提出してください.
おつかれさまでした