計算情報学２ 鈴木泰博

第5回

概要 前回はゴルフのパッティングのように関数・方程式により与えらた地形を生かして，$f(x) = 0$ となる $x$ をもとめる方法として2分法，はさみうち法，ニュートン法を扱った．今回はパッティングのような”技巧”を使わない方法として逐次代入法に触れる．ここでとりあえず解を求める方法は一段落．こっからさき，補間・数値積分・微分方程式の数値解法までは考え方は一本道である．今回は補間を解説する．

注意:このコースでの演習の多くには，「唯一の模範回答」はないと思ってほしい．もっとも数学の演習問題は正答が存在するが．前回の演習，これから行ってもらう演習ともに，３０名の受講者がいれば，３０通りの回答があってよい（間違っていればハナシは別だが..）．

課題のすすめかた：今回の課題は１問づつNUCTにいって回答するとは違った方法をとる．

1. まず，テキストエディタ（WORD, メモ帳，emacs, vi, atom.. なんでもよい）をひらく

2. 課題1から順に回答していく．資料を順に読み進めていくと，課題が出てくるので，その回答を書き足していく

3. すべてが終わったら，NUCTから添付ファイルで提出する．

   ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

4. 締め切りは，原則として翌週の水曜日である（例外もある）．締め切りには注意する．締め切りを過ぎたら提出できない．９割以上の受講生の方々はきちんと，フォーマットも締め切りも守っている．

5. 締め切りが過ぎたら提出できない．課題はすべて評価しC以上であればカウントする．Fの場合にはカウントにならない．

   ＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

逐次代入法

逐次代入法とは方程式 $f(x) = cos(x) - x$ の解を求める場合，

1. まず $f(x)$ を，$x = f(x)$ に変形する．
2. $x = f(x)$ を $x_{k+1} = f(x_k)$とする．
3. 初期値 $x_0$ から$x_1$をもとめ，$f(x_1)$から$f(x_2)$をもとめ...以下繰り返す．

このように，順繰りに$x_k$を代入していく方法が逐次近似法である．

どこで計算をとめるのだろう？ $x_k$と$x_{k+1}$の差が小さくなったら「収束した」とみなす．どれぐらいの差になったら収束とみなすか？が精度になる．ではさっそくやってみよう．上図ですでに出題しているが．

課題１：$f(x) = cos(x) - x$を逐次近似法（上図では逐次代入法と書いてありますが）により求めよ．これは手では計算できないので，プログラミングするかEXCELにより計算せよ．

逐次近似法の”数学的解釈”

逐次近似法はとても単純な方法だ．この方法を”数学的に解釈”してみよう．この「数学的解釈」というのは数理科学でよくおこなう方法である．これはある数式が得られた場合に，それの数式を数学的に”見直してみる”という行為を，数学的解釈とよぶ．

数学的解釈とは：たとえば，前回に「はさみうち法」を扱った．そこでの区間 $[a, b]$で $f(0) = c$ なる点を求めた．そのため $f(x) = 0$ となる $x$ について解いた．ここまでの数式の変形はあくまでも $f(0)$ となる $x$ を一般的に求めたわけである．ここで一旦それまでの”気持ち”から離れて，得られた式を「解釈」してみると，内分点と解釈できる，ことがわかる．このように得られた数式を「解釈しなおす」というのは，数理科学で重要な方法である．

　ほかにもたとえば，運動方程式 $f = ma$ は@「質量 x 加速度」が力であることを示した方程式だが，これは $f = ma = \frac{P}{dt}, P = mv$ と「解釈」することができる．ここで$P$とは運動量のことなので，運動方程式は運動量の時間変化と「解釈」することができる．

では，逐次近似法の数学的解釈をしてみよう．逐次近似法では数式を

$f(x) = x$

とする．方程式や関数の解はどのようなかたちか？以前になんども”念を押した”ところだ...$f(x) = 0$となる$x$が解であった．逐次近似法はそれを$f(x) = x$とするわけだ．これはどのように数学的に解釈できるだろう？逐次近似法のアルゴリズムをもういちどみなおしてみよう．

i). $x = f(x)$ を $x_{k+1} = f(x_k)$とする．

ii). 初期値 $x_0$ から$x_1$をもとめ，$f(x_1)$から$f(x_2)$をもとめ...以下繰り返す．

このなかでポイントは $x_{k+1} = f(x_k)$の部分である．

課題2 $x_{k+1} = f(x_k)$を”数学的に解釈して図示せよ”．この問題は「考えてみると面白い」課題なので，興味のあるひとは，ぜひじっくり考えてみてほしい．

課題２での $x_{k+1} = f(x_k)$ はけっこうスゴイことをやっている．この数式を日本語に翻訳すると，

1. $f(x)$に $x_k$ を入力して$f(x)$の出力を計算する

2. 得られた出力を入力にする．つまり「出口と入口を直結させてしまう」（えーっ！）

3. 1. にもどる

コンピュータにたとえれば，計算した結果が出たらそれが入力になって，その結果が出たら，それが入力になって．．とのプロセスが延々続くわけだ．

どうしたら出力を入力につなぐことができるのか? この操作を数学的に記述すると，

$出力 = 入力$

とすればよい．つまり，

$f(x) = x$

とすればよいことになる．これを幾何学的に書いてみると

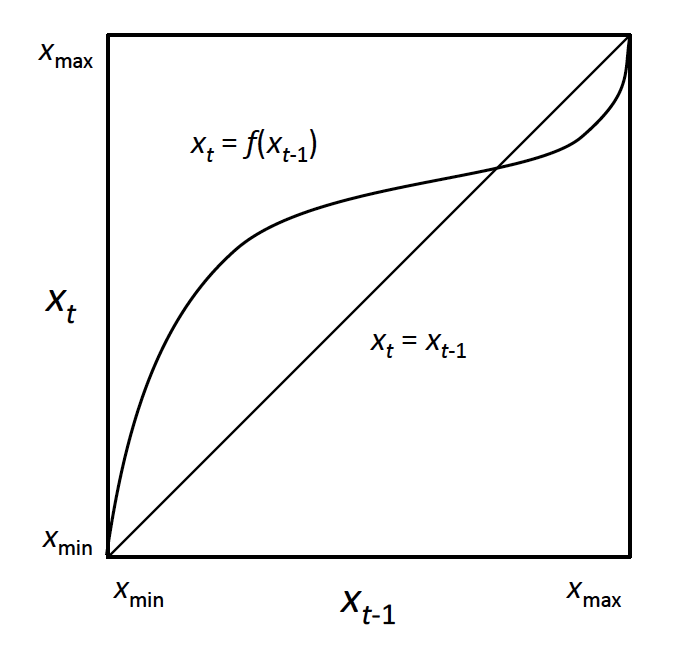
となる．上の図の対角線はなにか？これが $f(x) = x$である（えっ？とおもうひとは，$y = x$と読み替えてみればよい．これは慣れ親しんだ切片０の一次関数のこと）．

これで $f(x_{k+1}) = x_k$ を図示することができた．

演習 （これはノートや紙で行なってください）提出の必要はありません．自分の理解のための課題です．

1) ノート上に，この図を描く．

2) 適当な初期値を決めて $f(x_0)$ を図示する．そのため，

1. x_0$から$f(x)$ に向かって上に垂線を書いて，

2. $f(x)$との交点で”垂直に左折して”そのまま$f(x)$の軸との交点まで線を伸ばして交点をつくる

3. $f(x)$ 上にできた交点から$x$軸に平行に線を伸ばし，$f(x) = x$ との交点で，直角に右折して$x$軸との交点をつくる．

とする．ここで3.でもとまった$x$軸上の点が$x_1$である．これを繰り返すと，蜘蛛の巣，のような図がつくられる．このようにして得られる力学系を Cobweb 力学系とよぶ．

課題３が自力でできなかった人は以下に答えがある．これは，動かしてみて「おーっつ！」というところが”醍醐味”．これをやってみると$f(x) = x$ が「鏡」の役割をしていることがわかる．$f(x)$ を $x$に写し，$x$を$f(x)$に写している．

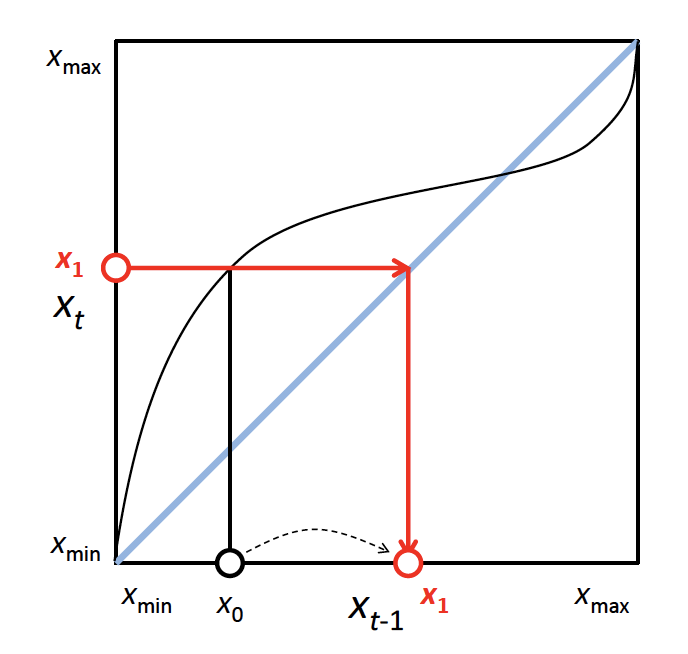
課題3 $f(x) = cos(x) - x$により解に至るまでをcobweb dynamicsとして図示せよ．WORDやパワポでつくってもいいが，手書きのノートを写メして，それをWORDに貼り付けてもいいとおもいます．

Cobweb力学系については日本語の参考文献はほとんどない．このコースの指定参考書のp68に解説があるので，参考にしてほしい．参考書へのリンク

補間

これまで，関数がない世界（ルール力学系）の世界から，関数で規定された世界（非線形方程式の数値解法）をへて，補間とは限られたデータから，その世界をつくっている関数，を推定する方法である．

なぜ関数を推定するのか？それは「予測がしたい」からである．

わたしたちは未来のことはわからないが，過去のデータはもっている．すると，やれることはひとつしかなくて，過去のデータで未来を予測する，しかない．このときによくある予測のしかたが「線形予測」である．センケイヨソクとはなにか？...字でかいてあるとおり「直線」で予測する．上図のように，過去から現在までの棒グラフでかいて，過去から現在の棒グラフの頂点を直線で結んでしまう..そしてその直線を未来に向かって伸ばしてしまう．そうすると100年後でも予測ができる！わけだ（えーつ！！！）．でも，この線形予測は世間を跋扈していて，ほとんどの未来予測（だいたい暗惨な将来が予測されるわけだが．．）は線形予測である．

「えっと，さっきまで”関数”を予測するってはなしていなかったっけ？」

「はい，そうです．線形予測とはつまり，過去のデータから線形関数を求めること，なのです」

ほとんどのデータは離散量です．なので，離散のデータから連続の線形関数を求める．．．これを線形補間といいます（補間．．間を補うので補間）．これをまとめると，以下のようになります．

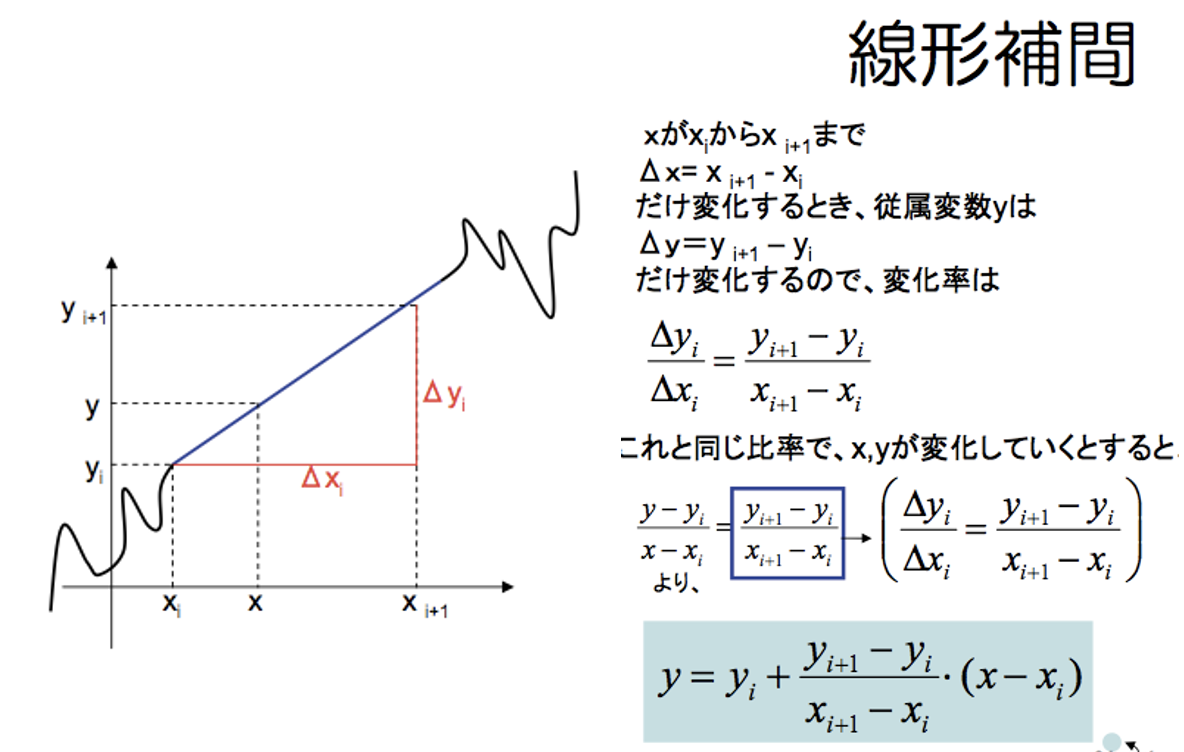
今回はここまでです．

課題をNUCTから提出してください．締め切りに注意！

おつかれさまでした．