情報リテラシー
第13回 表計算ソフトによる情報処理(基礎)
データサイエンスとはなにか?
データサイエンスは近年になってその重要性が認識されるようになってきました.この動きは以前にとりあげた「データジャーナリズム」とおなじ流れです.データジャーナリズムはデータサイエンスのジャーナリズムへの応用といえます.
データサイエンスは「データの取得」→「データの分析(統計学)」→「情報表現(インフォグラフィック)」で構成されます.ここで,インフォグラフィック,という見慣れないことばがでてきました.
インフォグラフィックとはデータ・データ分析の結果を,図像をもちいて表現する方法です.インフォグラフィックは近年一般化してきています.たとえば,以下のインフォグラフィックでは,自家用車に関する多くの統計データを物語風に表現しています.
データサイエンスは決して「理系」の分野ではありません.データサイエンスと縁が遠く感じるかもしれない,文学研究や歴史研究などの文献学でも,データサイエンスの手法がふんだんに使われるようになっています.
みなさんはヴィトゲンシュタインという哲学者をご存知でしょうか?以前に学会で,ノルウェーのベルゲンに行ったとき,友人に誘われて,ヴィトゲンシュタインのアーカイブ(文献施設)を訪れたことがあります.ベルゲンはヴィトゲンシュタインがショルデンというフィヨルドの奥部の小屋で執筆をしていたことで知られています.
https://twitter.com/i/status/953199559215259649 (ショルデンの彼の小屋の跡だそうです)
ふらりとアーカイブを訪れたのですが,とても丁寧に対応してくださいました.そして申し訳なさそうに「大変申し訳ないのですが,ここには直筆の原稿はないのです.すべて電子データに変換したものですから..」とおっしゃられ,どのように彼の文献を電子データに変換したかについて丁寧に教えていただきました.
文献学の専門家というと,膨大で詳細な文献に関する知識と圧倒的な記憶力に畏敬の念をもってきました.たとえば欧米の一流大学での哲学博士取得のための口頭試問では,たとえば「ヴィトゲンシュタインの,何々はどの文献のどこに書かれているか」のような問題が出されると聞いたことがあります.ですが,電子データ化されてしまえば検索すれば瞬時に,間違いや漏れがなく,わかってしまいます.
データサイエンスの方法
総務省統計局は「データサイエンス・オンライン講座」を毎年開講しています(受講料無料).コースの主な内容は「統計学の考え方とデータの見方」です.
データサイエンスことはじめ
先週から行なっているEXCELの実習を兼ねて,データサイエンスの基礎を学習してみましょう.といっても,数理統計学の理論を扱うわけではありません.今回扱うのは「平均と標準偏差」です.データサイエンスを行なう上で重要なことは数式を追うことではなく,使用する統計手法の意味,をよく理解していることです.
平均と標準偏差の統計的な意味は「データのばらつき」です.データサイエンスは,そのデータについての特徴を示したいわけです.特徴にはいろいろなものが考えられますが,そのひとつはばらつきです.データが同じような値で塊になっているのか,まったくバラバラに散らばっているのか,などを数字としてあらわしたいのです.数字としてあらわすことにより,感覚的ではなく合理的かつ客観的に比較検討ができるようになります.
では,さっそくはじめましょう.エクセルを起動させてください.
ワーク1:平均とはなにか?
1.セルに1から5までを記入してください
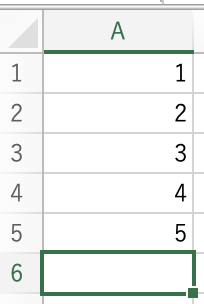
- これらをすべて足し合わせてください.

まず,エクセルで数式を扱うときには,セルに"="と書きます.このとき,英数モード,で=を記入します.
つぎに,A1(上図の水色)のセルを選択します.すると,
=A
となりますので,このよこに + を入力します.すると
=A+
となります.ここで,A2(上図でピンク)を選択します.すると,
=A1+A2
となります.これを繰り返していきます.そして,
=A1+A2+A3+A4+A5
まできたら.リターンを叩きます.すると合計が出てきます.

つぎに,平均をもとめるので,A7に=を入力します.
そして,合計が表示されているA6のセルを選択します.すると
=A6
となります.これを5で割れば平均が計算できますから,
=A6/5
とします.これで平均が計算できました.
ワーク2:平均からの差
このデータ1,2,3,4,5のバラツキを数字にするために,各々のデータの平均からの差を調べてみましょう.
そのためには,各々の値から平均を引けばいいですから,
まず,B1に=を代入して,A1を選択します.すると,
=A1
となります.つぎに,平均の入っているセルA7を選択して,
=A1-A7
とすれば,差が計算できます.
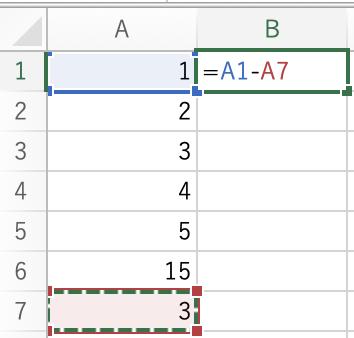
以上をB2からB5まで繰り返すと,平均からの差が計算できますので,すべての差を計算してください.もう少し進んだ方法をTipsで紹介します.余裕があるひとはやってみてください.
Tips: 絶対参照 平均からの差の計算を,以上のようにひとつずつ行なってもいいですが,データ数が増えると大変です.そのような時には絶対参照をつかうと便利です.やり方は,最初はおなじでB1に=を代入して,セルA1を選択します.
=A1
そして平均がはいっているセルA7を引くのですが,このセルは何度も使います.このように,同じセルを何度もつかうときに絶対参照をつかうと便利です.やりかたは,
=A1-A7
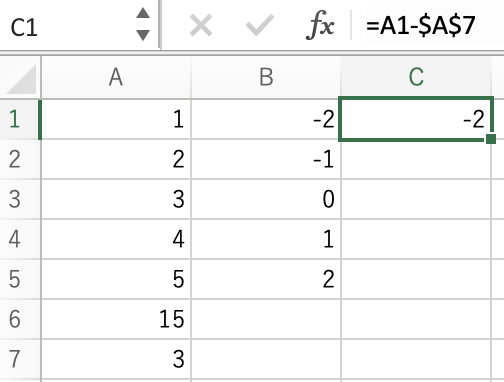
とA7を選択し,ファンクションキーの「F4」を押します(Macをつかっているひとは,fnキーを押すと選択できます).すると,
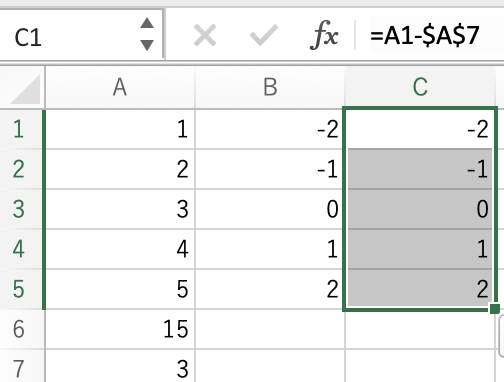
となります.$A$7が「絶対参照」です.
あとは,C1セルの右下ヘリの■をB5までドラグするだけで自動的に計算されます.
では,平均からの差をすべて足し合わせてください. 方法を忘れてしまったひとはワーク1をみなおしてください.
平均は重心
そもそも平均を計算したのは「データのばらつき」を数量化したかったためでした.でも...これではあまり意味がありませんね..たとえば,
a) 10,20,30,40,50
b) 1, 2,3,4,5,165
はいずれも平均は30で同じになってしまいます.a)は30を中心にして,等間隔に散らばっているのに対sて,b)はほとんど1から5にデータが固まっているのに,165という値のために,平均が大きくずれてしまっています.
これは,平均が全データのバランスをとる,重心,になっているからです.a)とb)ではデータのバラつき全く違います.なので,なんとかその差を数字にしたいのですが..どうしたらいいとおもいますか?
ひとつの考え方は「バラつきの平均をとる」ことです.バラつきの平均をとれば,a)とb)のちがいは示せそうなのですが..
統計ではこういった場合(足したらゼロになってしまうような場合)には,データを2乗します.そうすれば,正負がなくなるので足してもゼロになりません.
バラつきの平均を計算する
まず,先ほど計算した「平均からの差」を2乗りしましょう.まず,C1のセルに=を代入します.エクセルでは2乗は ^ を使うと計算できます.たとえば =2^2 とすれば2の2乗,=2^3とすれば2の3乗の計算ができます.

=B1^2とすればB1セルの2乗が計算できます.あとは,右下の■をC5までドラグすると自動的に各々のセルの2乗が計算できます.
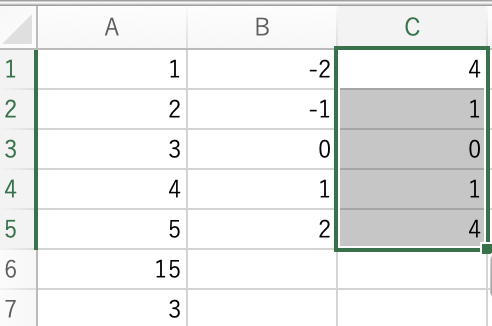
あとは,C列の値を足し合わせて平均をとるだけです.
やってみてください.
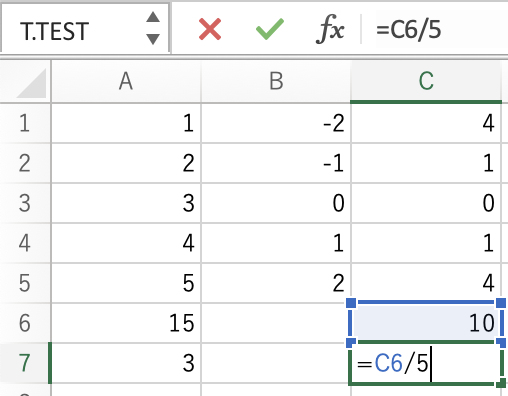
これで,ゼロにならずに「平均からの差を2乗した値の平均」が求められました.
偏差: 統計学では今回での平均のような一定の値からの差のことを偏差といいます.そして,
平方和: 2乗した値の和を平方和といいます.
なので,いままでの計算を統計学っぽくいうと「偏差平方平均」となります.この値は統計学では分散といいます.分散は2乗した値の平均になっているので,そのままデータと比較すると大きな値になってしまっています.
なので,ルートをとれば,もとのデータと同じような値になります.2乗した値のルートととると2乗する前の値になりますからね.2の2乗は4ですが,4のルートは2になりますから.では,求めた分散のルートととってみましょう,
エクセルでルートはsqrtという関数でもとめられます.使用上の注意は
=sqrt(
と ( をつけてからセルを選択します.そうしないとエラーになります.
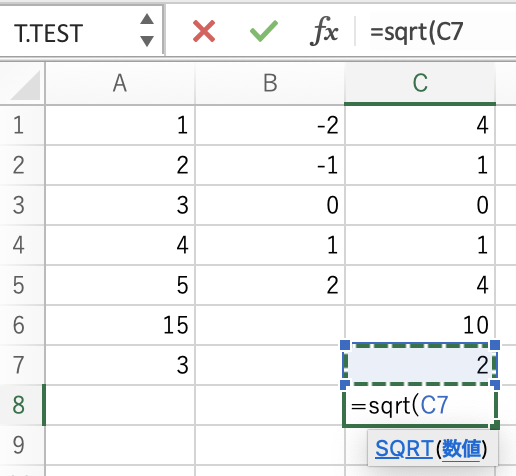
これで$\sqrt{2}=1.41421356$がもとめられました.この値のことを標準偏差といいます.標準偏差は2乗した値(分散)と違って,データとそのまま比べられます.
たとえば標準偏差をつかって今回のデータ 1, 2, 3, 4, 5 のバラつきを示すと
$3 \pm 1.41$ にデータがバラついている
のようにいえます.この標準偏差は統計学の基礎となる最も重要な値のひとつです.
標準偏差による評価
では,標準偏差をつかって先ほどのデータb)のバラつきを評価してみましょう.
b) 1, 2,3,4,5,165
いままでと同じように計算してもいいですが,エクセルには標準偏差の関数 stdevがありますので,これをつかえば一発で計算できます.

このように =stdev 入力すると,エクセルのバージョンによっては,複数の関数が表示されるかもしれません(されないかもしれませんが,それはそれで構いません).もし複数の選択があればSTDEV.P もしくは STEDVを選択してください.そして,( をわすれずに記入します.
つぎに,計算するデータをすべて選択します.

すると.標準偏差が計算できます.
a) 10,20,30,40,50
b) 1, 2,3,4,5,165
は平均だけをつかうと同じ値になってしまいましたが,標準偏差で比較すると60倍程度違っています.なので b)のほうがデータのばらつきが大きいことが数量化できました.
課題: 今回のワークで計算をしたエクセルファイルを添付して提出してください.
おつかれさまでした.