複雑系計算特論１および２　第5回

鈴木泰博

前回の課題を出題した背景には以下の論文がある．そもそもは，P.Davisとの「遊び」がはじまりだったが，その後に再び，このモデルをつかって遊んでみたらニューラルネットをつくることができた．

[1] Y. Suzuki, Neural Networks by using Self-Reinforcement Reactions, DOI:10.5954/icarob.2017.os17-2Corpus ID: 44189690

超簡単だけど，これはこれで面白いモデルなので，線形分離問題をこのニューラルネットで解いてちゃんと動くことを確かめておいてから，PCの音声入力にFFT（周波数分析）をかけて，線形分離問題を自動生成するようにして，それをこのニューラルネットで解くようにしてみた．そして，そのPCをもってカフェなどにいって，動かしていると，店員さんやお客さんの動きなどのノイズがどんどん，線形分離問題に変換され，それをバリバリ解いていくニューラルネットができる．これを”連れて”「これは「おお，がんばってるなぁ．．」というかんじで，おもしろい．

でもまぁ．．ただひたすら線形分離するだけなんで．線形分離問題をひたすら解いているPCと”コミュニケーション”をとりたくなって，ニューラルネットで線形分離問題を解くのではなく，簡単な音声合成を行うようにしてみた [2] . これはPCに話しかけると，わたしの音声をニューラルネットが学習して「なんか言い返してくる」ようなものだ．このシステムのサンプル・ランをしているときは，PCににむかって，低くうなったり，ミルクのなかにいる虫を発見した子供のようなモスキート音（聞こえないぐらい高い声）で叫んだりすると，PCが，聞くに耐えないようなノイズで言い返してくる．．さらに，わたくしがPCにむかって唸り返す．．といった．．PCと唸りあっている状態．深夜というか夜が明けてきそうな時間に家で”サンプルラン”をしていたら．．トイレに行く家族に”発見”され，ドン引きされたが．．

たしか，どこぞの学会で「デモ」をしたことがあったような．．記憶が．．３年前なのに記憶がはっきりしないあれは国際会議だったのか，なにかの報告会だったのか．．そのときの前の方に座っていたかたの”ひきつった笑顔”が思い起こされる．．「あー，こりゃ，えらいこと全員が”ドン引きしているな”．．」という．．空気感だけを鮮明におぼえている．．

[2] Y. Suzuki, Artificial Chemistry with sound wave, DOI:10.5954/icarob.2017.os17-3Corpus ID: 44102037.

脱線しすぎて，出発地点にもどってきた感があるが．．あのね，ここまでで「半分」ぐらいで，じつはさらに先があるんですわ．で，その半分が，南方熊楠の哲学をベースにした計算系（抽象的な化学反応系だとおもっていただいて結構です．物理化学的にも厳密にそうなので..）．この抽象化学系を，ポリヤの壺のネットワークとつなげるのが「残り半分」．つまり，２つのまったく異なる力学系をカップリングしてしまうわけで．．．「なんか複雑になりそうでしょ？」．

脱線のついでに，「ニューラルネットワークや進化計算はすでに確立されている」これは確かなことであり，それにとても興味があれば研究すればいい．だが，一方ですでに確立されている概念・技術を使うとは，立場としては「ユーザー」である．もし研究を志すとしたら．．ですが，あくまでも，自分の研究としてニューラルネットや進化計算を使う場合には「自分はユーザーであること」を認識しておくことが大切だと思います．勉強するためには，ユーザーとしてある程度その世界に慣れる必要はある．ですが，スーパーユーザーを目指すのもひとつだけど，全く新しいニューラルネットワークみたいなもの，や，進化計算らしきもの，を創造していくことも大切だと思います．

閑話休題．

計算の再定義

このコース資料では，計算の科学史からははいって，思いのほか，ライプニッツについて厚く語ってしまったので，戻れなくなって，南方熊楠までいくしかなくなってしまった．不眠でお困りのかたがいたら，ライプニッツのくだりを語って聞かせ，たちどころに熟睡させる自信がある．こちとら，積年の社会実験の結果がある．この流れでの講義をしてなかったのは，例外なく，1,2分で受講者の大半が白目になってきて10分後には，全員が熟睡してよだれをたらし，机のうえに突っ伏しているところで80分近くも，語り続けることになるからだ．それでもなぜ，語り続けるかというと，ほぼ全員が爆睡しているなかで，ほんの１，２名が「目を爛々と輝かせて，こっちに突っ込んでくるぐらいに前のめりに」聞いているのでね．

というわけで，途中ではありますが，ここで，計算の再定義をしておきます．計算機科学に不慣れで，チューリングのことをあまり知らないひと，また”「チャーチ・チューリングの提唱」や「ゲーデルの不完全性定理」とは，人間の知の限界を示したものである”という言明を「まぁ，そうだよね」とおもえちゃうかたは，こっから先は，理解不能，になるので，すこし自分で調べて予習してください．

はじめに

八百屋さんに行って，ジャガイモと人参とタマネギをカゴに入れてレジにいけば，レジスターに最初は0円と表示されていた合計金額の値が，ジャガイモ，人参，タマネギの代金が足されていくことで合計金額は変化していき，やがてすべて足されて最後に消費税が合算されると，それで合計金額は変化しなくなる．このように作用（足し算）により変化した状態（合計金額）のことを正規型とよぶことにする．正規型はこの例のように状態が変化しなくなった場合だけとは限らず，たとえば，円周率を求める場合には状態は変化しつづける．

よって正規型は 1 つになるとは限らない.例えば，足し算と掛け算の優先順位がないならば 2 × 3 + 4 の正規型は {10, 14} となるし，円周率を求める場合は {3, 3.1, 3.14, ...} と無限集合となる．以下では,特に指定しない限りは正規型とは正規型集合をさすことにする.

アルゴリズム・順序

物事が作用とともに変化する際に，あらかじめ作用の順番が定められていたり，変化の過程から作用の順位が生じてくるなど，作用が順序をもつ場合，その順序をアルゴリズムとよぶ．

八百屋さんの例では「ジャガイモ十人参十タマネギ」とそれぞれの価格の足し算の順番がアルゴリズムなるし，計算機のプログラムはアルゴリズムとなる．他にも，たとえば化学反応は相対的に速度の順位が生じ，その反応速度の順位によって反応状態が変化するので，その順位がアルゴリズムとなる．

アルゴリズムの順位を変えることをプログラミングとよぶ．たとえば，ジャガイモを4 個とタマネギを 1 つそして人参を 3本買った場合，これらをひとつづつ足していくのでは効率が悪いので「ジャガイモ×4 + 人参 ×3 + タマネギ」のように，足し算をまとめて掛け算にして，作用と順序を変えることがプログラミングに相当する．化学反応ではある反応速度の順位を変えるために，触媒や酵素が用いられるが，それもプログラミングとなる．

観測と検証

アルゴリズムにより変化した物事について，それを観測する仕方が定められている場合，その系は計算となる．

観測はあらかじめ定義された正解集合と正規型集合の積集合 (AND)と定義される．この積集合に＾まれる要素が正解候補となる．例えば，粘菌を用いて迷路の最短経路探索を行う場合，正規型集合は一定時間後の粘菌の状態となる．入り口から出口まで到達している場合もあれば，途中で止まってしまったり，複数に分裂したり，入り口で止まってしまったりとさまざまな状態変化がみられであろうが，それらはすべて正規型である．

ここで正解集合を「入り口から出口まで到達している個体」とすると，正解候補はさまざまな正規型のなかで，「迷路の入口から出口まで到達している個体」となる．これらは観測する計算主体からみれば少なくとも迷路に入って出てきていることになる．

一方で粘菌が「迷路を解こう」と行動したのか否かについては知る由もない．粘菌はただ状態変化しただけでありそれ以上でも以下でもない．なので「粘菌には迷路を解く知性がある」，「粘菌は賢い」との主張は粘菌の行動をそのように観測する計算主体の勝手な言い分である．もし計算主体の正解集合が「粘菌が 2 つに分裂する」であれば，今度は正規型集合には「2つに分裂した粘菌」が選ばれることになる．

観測によって正解候補として「入り口から出口まで到達している個体」が選ばれたわけだが，これらがすべて最短経路を通っているとは限らないため，正解候補の正当性の検証を行う必要がある．そのために，計算主体はあらかじめ迷路の最短経路長を調査し，正解候補のなかで最短経路長となっている個体を「正解」とする．

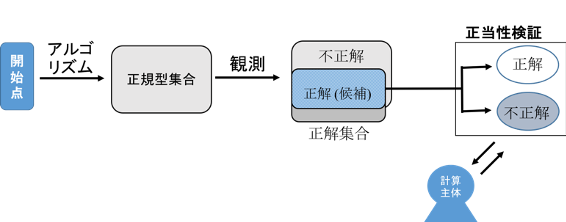
図 1.1 計算のプロセス: 計算を行うとまず, 正規型集合が得られる.その正規型集合の要素のうち,予め設定してある正解集合に＾まれたものが正解候補となる（ここが観測に相当）.そして, 正解候補の正当性の検証から正解が求められる

自明な計算は計算ではない

正解候補の正当性の検証を行う必要がない場合を，正解集合が自明であるとよぶ．その場合は観測が正当性の検証となるので観測結果が正解となる．粘菌による最短経路探索で，計算主体が最短経路長を知っていたならば，正解集合は自明で，正規型のなかから最短経路長の個体を選択すれば，それが正解となる．

さらに例えば 1 + 1 = 2, 2 × 2 = 4のように計算を行わなくても正解が得られるならば，つまり「アルゴリズムによる状態変化が生じない」場合は，計算が生じないことになるため，これらは計算ではない．

このように正規型集合が自明（アルゴリズムによる状態変化を要さない） で，かつ正解集合が自明な場合，つまり自明に得られた正解集合が正解の場合は計算は生じない．それらは，知識，代名詞，言い換え，（自明な）同値などといわれる．

客観的検証と主観的検証

正当性の検証を計算主体（計算を行なっている主体）の外で行う場合を「客観的検証」，計算主体自身が正当性の検証を行う場合を「主観的検証」とよぶ．ここでの客観的とは計算"主 "体に対しての" 客 "観（主・客）のことである．

図 1.2 計算のプロセス: 計算を行うとまず, 正規型集合が得られる.その正規型集合の要素のうち,予め設定してある正解集合に＾まれたものが正解となる（ここが観測に相当）.そして,正解の正当性の検証を行う（正解が検証により不正解となる場合もある，本文参照）

粘菌をもちいた最短経路探索は，粘菌という生物をもちいた計算であるが，検証は客観的に行われる（最短経路長により）．エーデルマン（Adelman）による DNA 分子をもちいたハミルトン経路を求める計算系や DNA 折り紙も客観的検証である．また計算主体がヒトではない場合，たとえば DNA複製系では複製結果は熱力学的校正などにより客観的検証が行われ，もし複製エラーによりタンパク質が失活した場合にも進化淘汰により客観的検証が行われる．

一方，コンピュータをもちいたグラフィクスや作曲などでは，作家の主観的観測により作品が制作されるので（正解集合の検証）主観的検証となる．

また，同一の計算主体であっても検証系の入れ替えにより，客観的検証と主観的検証を併用する場合もある．例えば，落語は原則として師匠から弟子に口承で教授される．弟子は師匠に教わった噺の記憶（近年では映像や音声データの場合もあるが）を正解集合として，何度も稽古して正解候補ができたら（覚えたとおもったら），師匠の前で演じてみせて，もし" これでよし"となったら正解となる（客観的検証，正解にいたることを" あがる "という）．もし，その弟子が教わった噺を改変していって「わたしはお前にそんなふうに噺を教えたつもりはないっ」と師匠連に叱られても（客観的検証で不正解），委細かまわず噺を変えていく場合には，変えた噺（正解候補）の検証はその弟子による主観的検証となる．

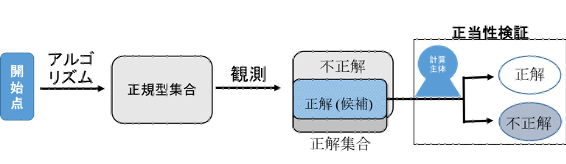
図 1.3 計算のプロセス: 計算を行うとまず, 正規型集合が得られる.その正規型集合の要素のうち,予め設定してある正解集合に＾まれたものが正解となる（ここが観測に相当）.そして,正解の正当性の検証を行う（正解が検証により不正解となる場合もある，本文参照）

検証と決定問題

客観的検証の場合，たとえば「作成したプログラムが停止するかを判断するかの検証」のように自己言及性がある場合はパラドックスが生じて決定不能状態に陥ってしまう場合もある．客観的検証では計算主体と検証系は独立しているので，たとえば検証作業が長引いている場合に「あと 10分で最終結論を出して欲しい．わからなければ，わからないと答えるべし」などと干渉することはできない．

主観的検証の場合，例えば計算主体が" プログラムの名人・上手"の場合の「作成したプログラムが停止するかを判断するかの検証」は，勘と経験から即座に決定される場合もあれば，100年の長考に入ることもあるだろう．いずれにせよ，即座に決定されるか否かは計算主体の主観的検証（気持ちひとつ）による．よって検証作業が長引いている場合に「あと10分で最終結論を出す．わからなければ，わからないと答える」などと計算主体自身やそれ以外の何かが検証系に干渉することができる．

とりあえず，今回はこのあたりでとめることにする．

今回の課題：

1) 自然系のなかには，この以上の「計算の定義」をもちいることで，計算系とみなせる現象がある．そのような自然現象を3つみつけて，この定義にしたがって（つまり，開始点，アルゴリズム，観測，正解集合などの，定義でもちいている概念にあてはめる），その自然現象を計算系として再定義せよ．

2) 1)の問題で構築した3種類の計算系を基に，自然系ではどのように主観的検証を行う計算系が，客観的検証を行う計算系へ進化するか考察せよ．