複雑系計算特論１および２　第7回

鈴木泰博

基本的な圏論の定義に慣れたところで，圏論での「直積」を定義する．この定義をそのままつかうと「事」を解釈することができる．

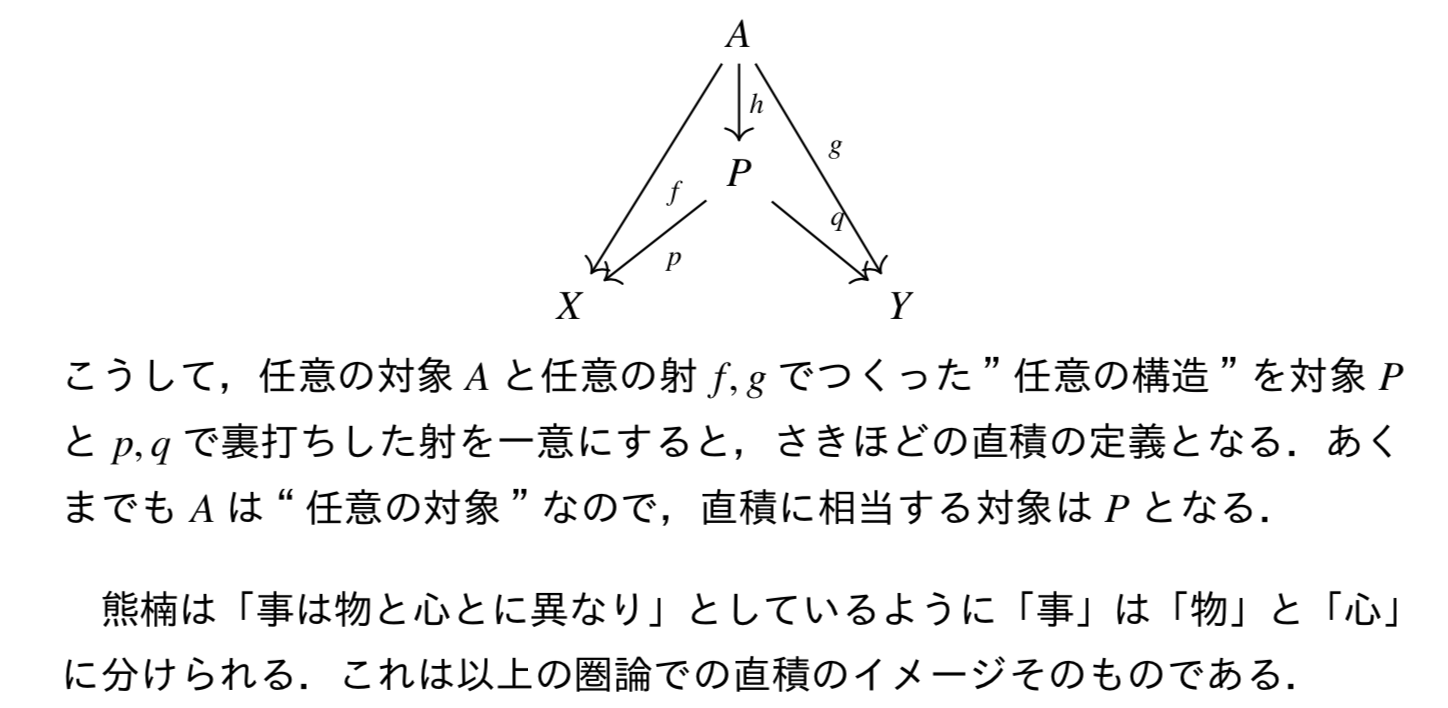
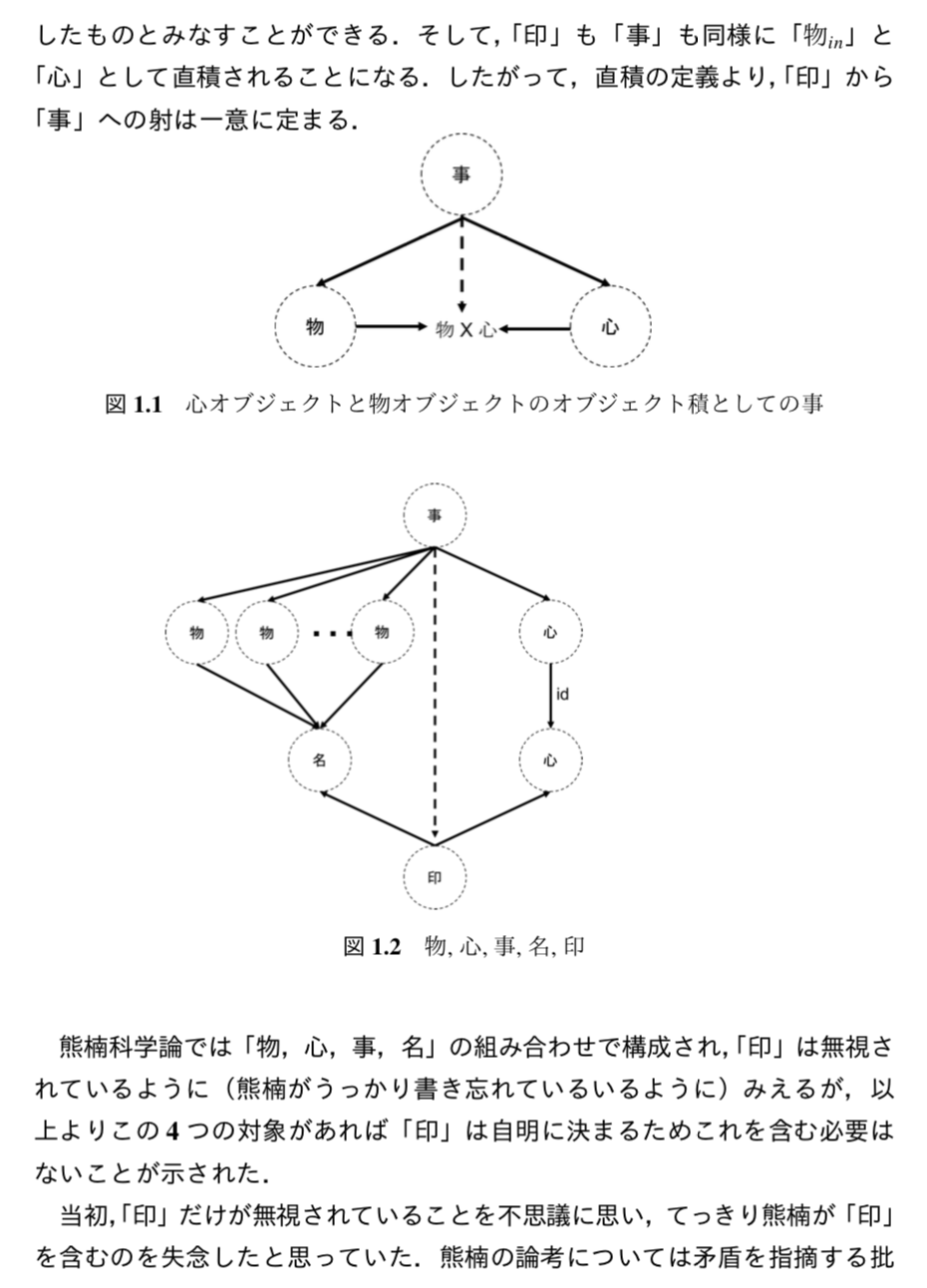
課題１

1. ”事の学”には数学が含まれるが，物理学は含まれない．その理由を「事」が「物」と「心」の直積で定義されることを踏まえて述べよ．
2. 「事」から「印」への射が唯一存在することを示せ（圏論の一般的な教科書の直積の項を参考にせよ）．

「事」の等しさ

課題２

1) 圏論でのモニック射をつかうと，上述した「物」の等さを記述できることを示せ．

2) 圏論でのエピック射をつかうと，上述した「事」の等さを記述できることを示せ．

以上の定式化により，以下の重要な帰結を得ることができる．

熊楠科学論の集合論

圏論では以上での「物」の等しさがモノ（Monic），「事」の等さがエピ（Epic）とよばれる．もし「物」と「事」の等さが一致する場合は，「物」と「名」はモノかつエピとなるがこれは数学的には全単射と同じ意味である．「物」から「名」への射がエピかつモノのときに，「物」から「名」への射に対してその逆射が存在するならば，「物」と「名」は同型になる．

「物」から「名」への射とは例えば，“ 緑色のお餅”（「物」）から“ ずんだ餅”（「名」）の射に対して，この逆射，つまり“ ずんだ餅”（「名」）から“ 緑色のお餅”への射である．この逆射が存在しない場合は構造がフラット（「物」のみで構成される圏のような）が多いが，本論の場合で例えば，赤色（「物」）と赤色（「名」）の場合には，逆射が存在しないようにみえるが，実際は「物」としての赤色（色紙や絵の具）と，「名」としての赤色であり種類が異なるため恒等射ではない．以上より熊楠科学論は「物」を要素，「事」を認識，「名」を代表元とすることで素朴集合論とみなすことができることになる．つまり「物，心，名，事」で構成される世界は集合論により記述される世界とみなすことができる．そこで，熊楠科学論のモデルとして集合上の因果計算系を構築する．この計算系ではすべては集合論的に記述され，因果律として記述される「事」により変化していく．

春１期の課題

以下の２つの課題のうち１つを選択せよ．

1. Self-Reinforcement Reactionsを発展させた創発計算系を構築せよ
2. 計算の定義を基に，自然のなかに計算系を見出して実際に計算系を構築せよ．

評価方法とルールは第１回で告知しているとおりです．

課題の評価基準

A+ : 独自に実験系や数理モデルを作成し，シミュレーションや理論的考察を行い結果をまとめる．

A : 実験系や数理モデルなどを作成し，計算機シミュレーションや理論的考察を行い，結果をまとめる．

B: 数理モデル，シミュレーションなどを行い結果をまとめる．

C: 数理モデル，シミュレーションなど行っているが，内容が乏しい．

F: 提出しているだけで，コース資料などをなぞっているだけで，内容がほとんどない．