複雑系計算特論１および２　第8回

鈴木泰博

春１期の総括

南方熊楠の科学論を基盤として「計算」の再定義を行なった．そして，熊楠の科学論の圏論による解釈から，「物」と「事」が等しい場合には「名」との関係が全単射となる．「物」，「事」，「名」の構成から同型射であることも明らかである．

同型射でないとは，「物：りんご」から「名：りんご」への射$f$と「名：りんご」から「物：りんご」への射$g$において$gf \neq id_g$ かつ $fg \neq id_f$ なので「りんご（物）を見て（心），”りんごだ！（名）”」と「名」が浮かんだとして（$gf$...関数合成なので順序が逆になることに注意 $g(f(x))$のイメージね )，逆に「りんご（名）」から「りんご（物）」を選別する」と，全く違うものになるということだ．

もっと噛み砕くと「りんごを見て，”あ，りんごだ”」と思っているのに，「長野から送ってきたりんごがあるんだけど食べる？」と，「名」としての”りんご”を指し示しているのに，「”はい，どうぞ”，とトマトを差し出す」ようなものだ．つまり「名」としてのりんごと，「物」としてのりんごが一致していないわけね．

ちょっと，こういった場合を考えてみましょう．

課題１　$f:$「物」から「名」, $g:$「名」から「物」の関係がエピックかつモニックであるが，$gf \neq id_g$ かつ $fg \neq id_f$ となるのはどのような場合か．

ヒント：自然計算と形式計算の違い，つまり観測の仕方，から考えてみるとよい．

課題１が解決されると（逆射が存在する）と，「物」から「事」を介しての「名」と，「名」から「物」への関係が同型になる．ここが，熊楠の科学論を基盤にしている本論の重要な点であるが，それは，

「物」と「名」の同型性は「観測，心」が決める．

同型という数学の概念は，数学という形式系のなかの客観的な概念である，が，本計算論では，「心」を基盤とした観測という名の主観が同型性の有無を決める．

課題１が成立すると，熊楠の科学論は，

• 「名」：代表元
• 「物」：要素

とする集合論とみなすことができる．たとえば，

• 「名」：りんご
• 「物」：無限ともいえる色も形も味も異なった果実

となるわけだ．でも，ここで「？」が湧いてくる．．．

「さっきまで全単射だ同型だと騒いでいて，課題まで出題していたくせに，「物」は無限の要素だと？！」

「そりゃあんた，全単射じゃないよ！，ほれ以下をみなさいよ．wikipediaにはこうなってるでしょ」

「でも．．集合の表記は$\{a,a,a,b\}$は$\{a,b\}$としちゃうよね？」

「そりゃあぁ．．だって，なんか，そういう定義だもん．．ごにょごにょ」

ここが「計算系」をつくっていく立場からして大変にグレーなところである．平気な顔をして$a$とか$a,b$とかゆっているが，わたしたちがやっているのは自然計算である．自然界では厳密に全く同じものなど，ほとんど存在しない．

なぜ集合論では{a,a}をaで代表させているか？そこには本当は「心」が介在している．そして，先週の課題で行なった「物の同一性」を前提にしているのだ．

熊楠の科学論は素朴集合論として解釈できるが，それは「心：認識」がない素朴集合論ではない．認識を含んだ素朴集合論なのである．「どうやって認識を入れた素朴集合論するのか？」については今回はイメージだけを述べて春2期にきちんと解説する．

計算系の構築

さて，ひとまず熊楠の科学論で基礎を構築することができた．では，この基礎の上に計算系を構築していこう（本格的には春２期からね．今日はさわりだけ）．

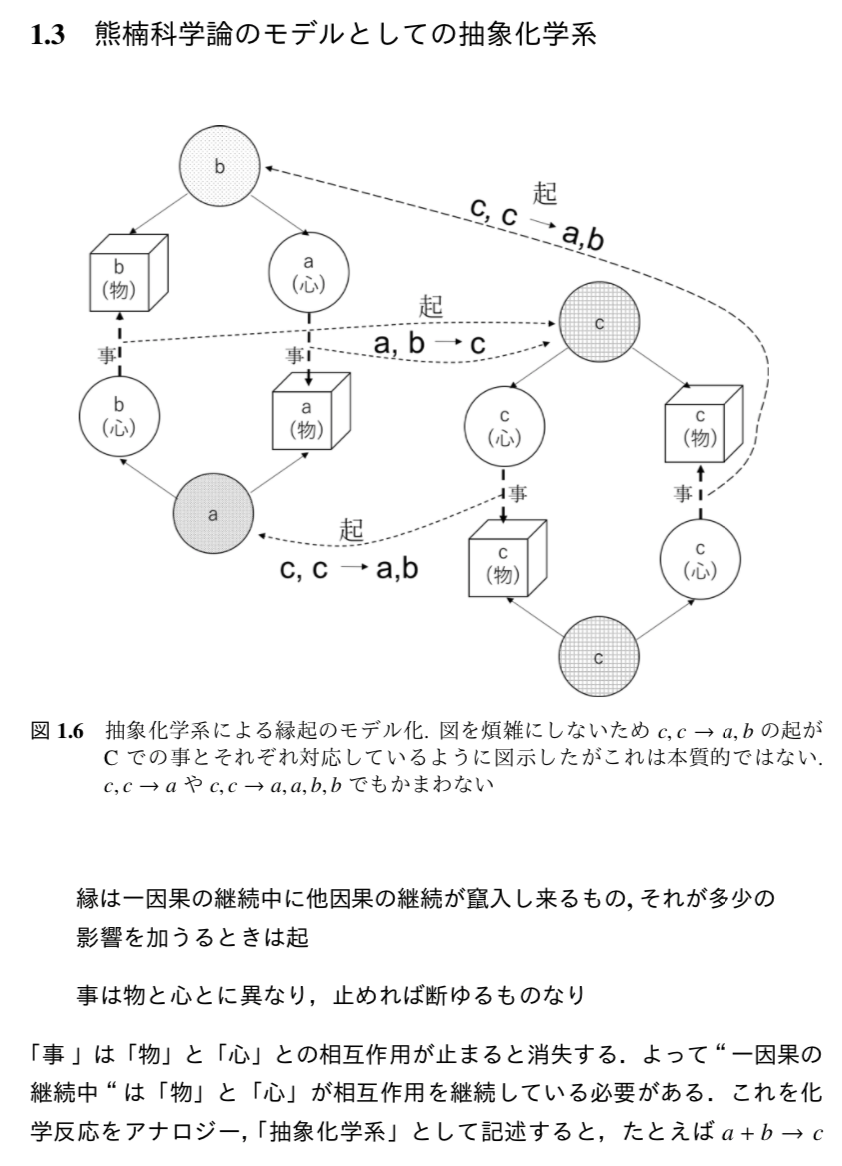
そのためには「縁起」の概念が重要になる．．．復習

この「縁起」を，実装しよう．

以上に概要を述べてしまったが，今回は「読んでおいてね」とゆっておこう．春１期の最後に，以前に南方熊楠の生家に取材にいったときのビデオでもみてください．場所は和歌山県の紀伊田辺．私は何度も取材に行って，熊楠の直筆原稿の調査や，熊楠が活動したフィールドの調査におとづれています．ちょっと時間がなくてナレーションを入れられないのだけど，ビデオは熊楠の生家（現在は「南方熊楠顕彰館」となっている）で，彼の重要なフィールドであった「庭」，彼の研究室みたいなものだった「居間」なぞの映像がある．

だが大変残念なことに，まぁいろいろあってね．．，熊楠の息吹はあまり感じられない．唯一，「熊楠の血」をかんじることができるのは，お孫さんが顕彰館のとなりの生家にいらして，実際にお話が聞けることかな．．

春１期の課題

以下の２つの課題のうち１つを選択せよ．

1. Self-Reinforcement Reactionsを発展させた創発計算系を構築せよ
2. 計算の定義を基に，自然のなかに計算系を見出して実際に計算系を構築せよ．

評価方法とルールは第１回で告知しているとおりです．

課題の評価基準

A+ : 独自に実験系や数理モデルを作成し，シミュレーションや理論的考察を行い結果をまとめる．

A : 実験系や数理モデルなどを作成し，計算機シミュレーションや理論的考察を行い，結果をまとめる．

B: 数理モデル，シミュレーションなどを行い結果をまとめる．

C: 数理モデル，シミュレーションなど行っているが，内容が乏しい．

F: 提出しているだけで，コース資料などをなぞっているだけで，内容がほとんどない．