複雑系計算特論１および２　第11回

鈴木泰博

概要： ARMSについて．

前回の課題の講評：決定論的ARMSでRK法を行うのは，難しい課題だったようである．完答できているのはごく少数であった．普通にRKで解いているようにしか見えなかった課題には，その旨をコメントしました．

ARMSをもちいたモデル化について，ごく基本的なことであるが再掲しておく．

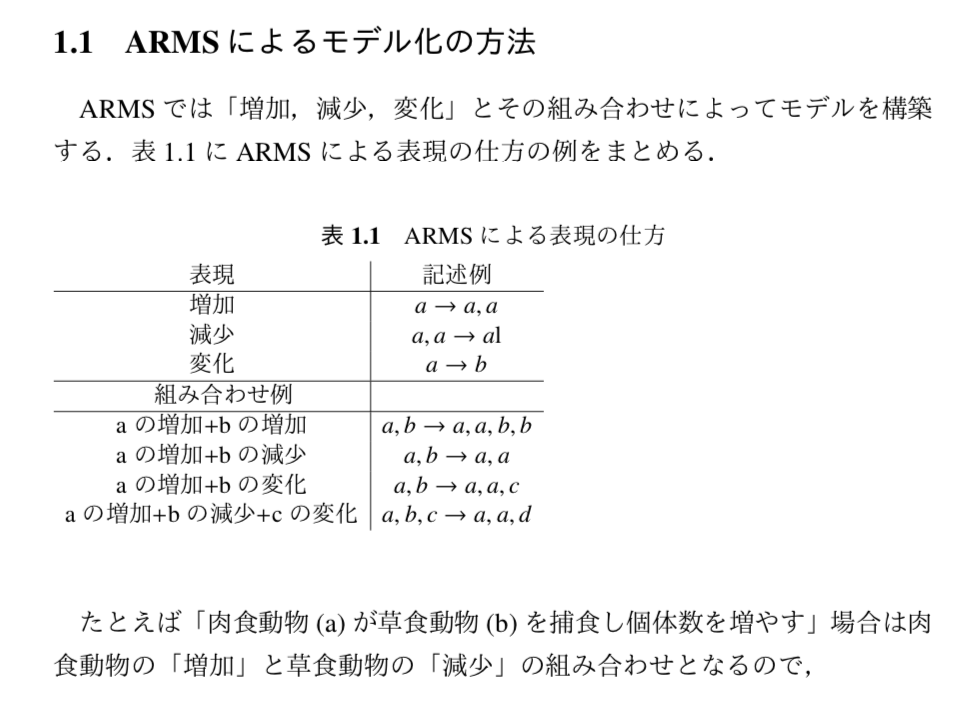
課題 LVモデルを決定的ARMSでルンゲクッタ法をもちいてシミュレーションしなさい．

一般計算科学

本論のミッションは熊楠の科学論にもとづく計算系をもちいて，アルゴリズムにより自然の理解である．この立場は，物理や数学と明確に異なる．

ARMSをもちいてさまざまな自然系を記述してきたが，それらは通常のシミュレーションとは異なる．一般計算科学での「シミュレーション」とは，熊楠の科学論のモデルであるARMSをもちいて自然のモノゴトを「縁起の連鎖」として解釈することである．

なので，ARMSでのシミュレーションの結果が観測されている現象と一致することは要請されるが，本当の要諦はその先である．

一般計算科学は物理でもなければ数学でもない．自然のモノゴトの仕組みを「縁起の連鎖」の立場から解明するのが，一般計算科学である．

これまで，ランダム化学系，Belousov-Zhabotinskii反応（非線形化学振動），生命の起源（化学オートポイエシス），細胞内シグナル伝達系（P53-MDM2系），化学生態系とミクロからマクロまでの自己組織化現象の記述を行なってきた．以下では生命の起源について紹介する．

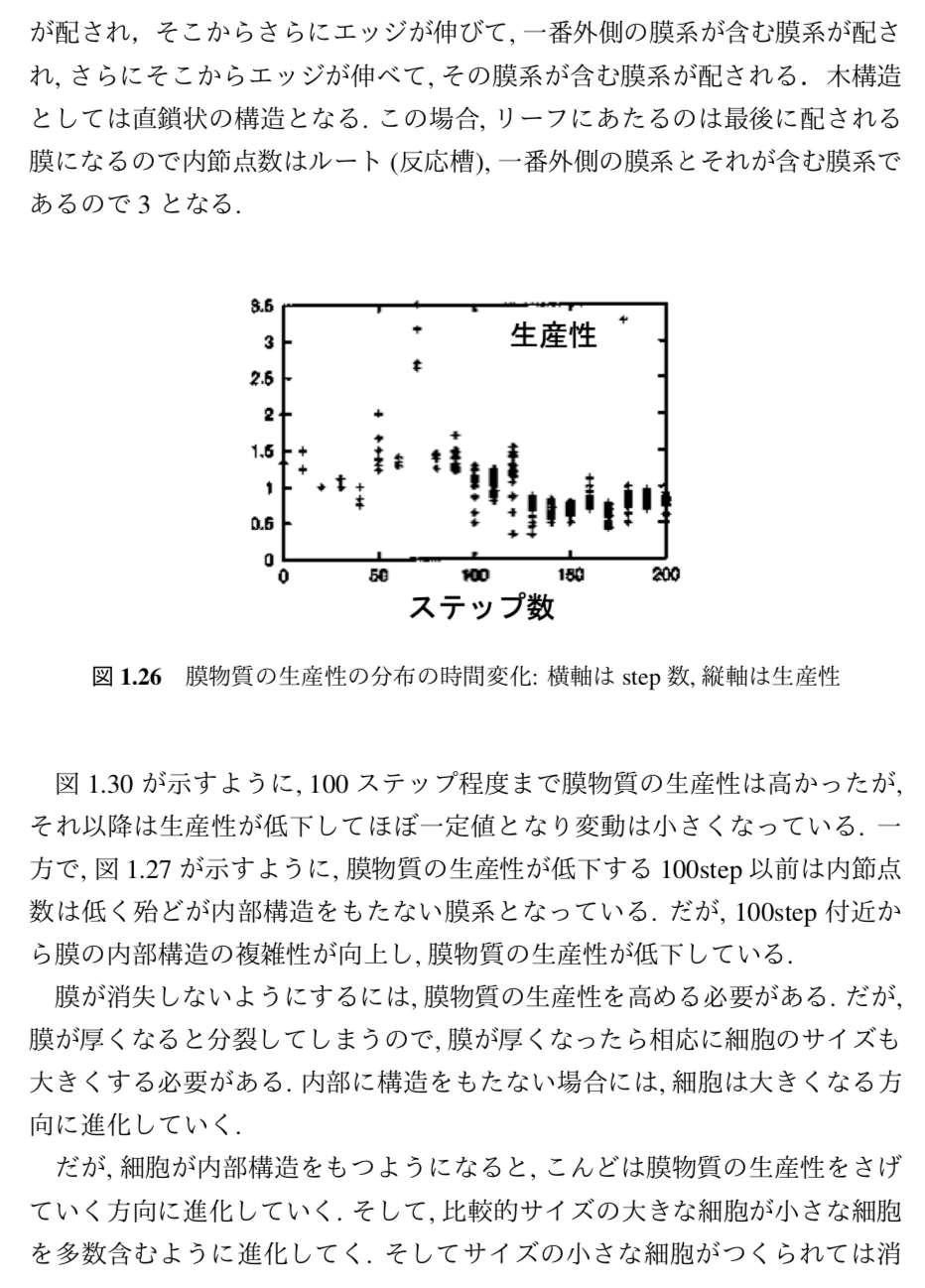
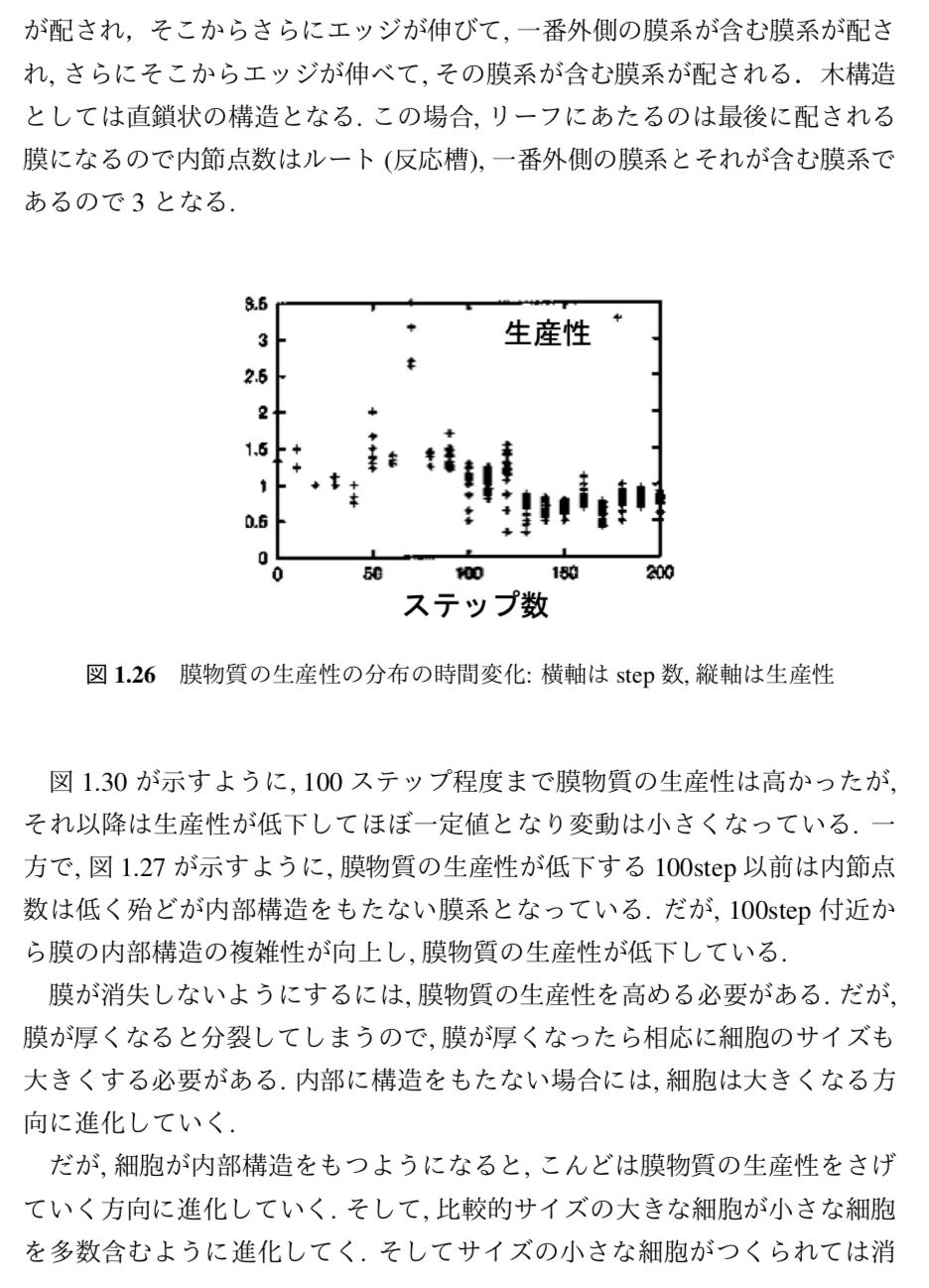
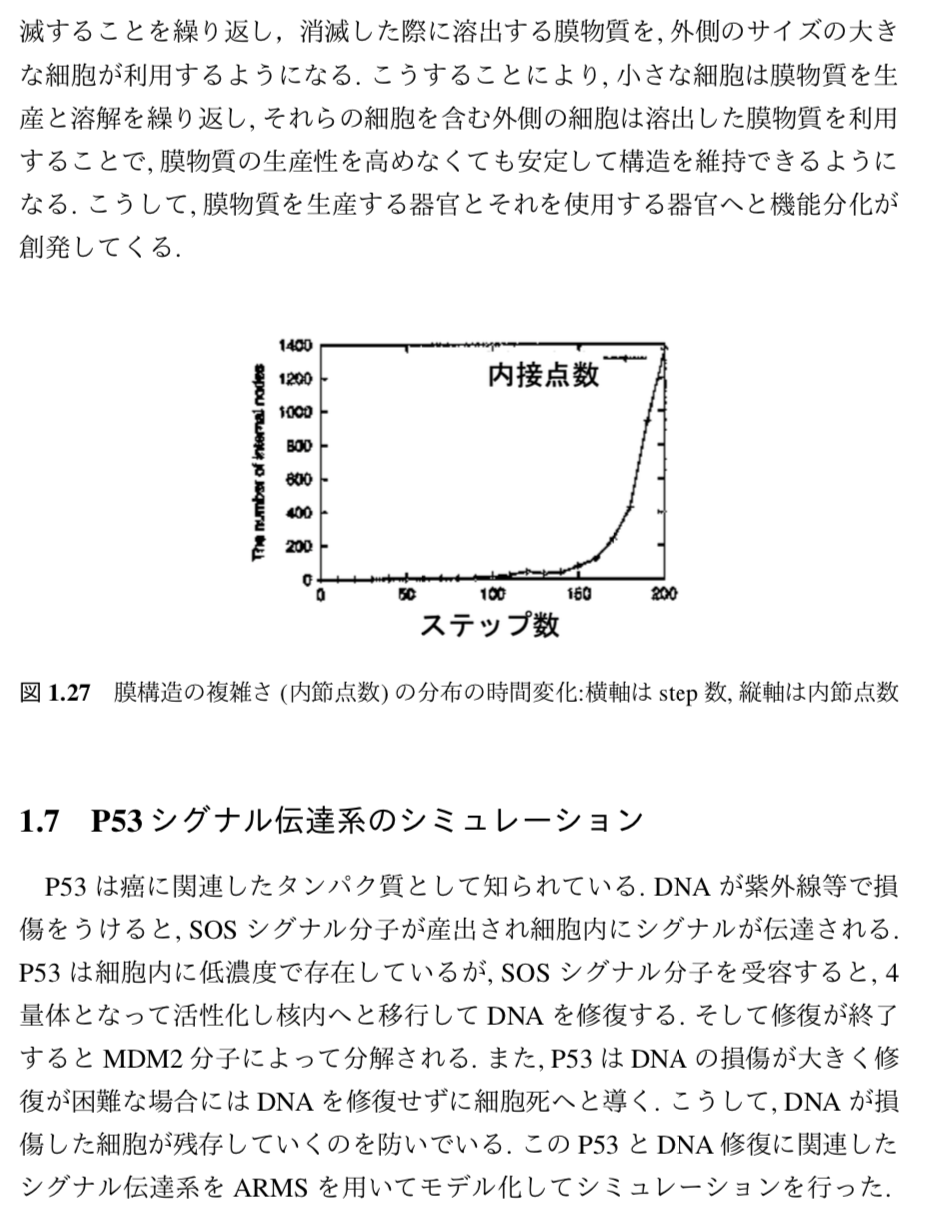
さまざまな自己組織化系のシミュレーションから，自己組織化を「縁起」として特徴づけた．それが「情報の散逸」である．

課題　

$\dot{X} = ax -bxy$

$\dot{Y} = bxy - cy$

このLV系は，

$\dot{X} = x(a - by)$

$\dot{Y}=y(bx-c)$

より，$(x, y) = (0, 0), (c/b, a/b)$の平衡点をもつ（代入すると$\dot{X},\dot{Y}$がともに0になることからわかる）．平衡点周囲の振る舞いは，$x, y$が平衡点より大きい/小さい場合の$\dot{X}, \dot{Y}$の符号の変化からわかる．

たとえば，$x >c/b$ かつ $y > a/b$ならば，$\dot{X} > 0, \dot{Y} < 0$になるので（代入してみればわかる），

以上を参考にLV系に情報の散逸を入れた以下の場合を考察せよ．

$\dot{X} = ax - b xyv$

$\dot{Y} = bxyv - cy$

今回は以上です．締め切りに気をつけてNUCTから課題を提出してください