第12回 情報の散逸の自然系への応用

大規模データには一般に偏りやノイズ含まれている．たとえば生物ビッグデータの場合，細胞一つをとってみても, それは広大な宇宙のようなもので探求すべきことには 限りがなく, 扱いに困るほどのデータを以てしてもデータ化されている部分はそ のごく一部に過ぎない. 大規模生物データは, 満遍なく詳細にデータがサンプリング されていることは極めて稀であり, 興味がもたれて いる現象や部位等のみに偏っている．また実験の手法によってはデータを合理的 に判断や分析す ることが困難なデータも多い.

例えば, 現在, タンパク質間相互作用の大規模データ解析には酵母ツーハイブリッ ド法（Yeast 2 Hybdid法, Y2H）がよく使われている. Y2Hとは喩えると, タン パク質の海に相互作用を知りたいタンパク質を餌として垂らし, その餌 で''釣れてくる（結合してくる）タンパク質を調べて相互作用を検出する実験 である. その場合に, タンパク質Aを餌にしてタンパク質Bが釣れたとしても, 逆にタンパク質Bを餌にしてもタンパク質Aが釣れてこないことも多い. また, Y2Hは一般に細胞をつくっているタンパク質を全てバラバラにしてから実験を行うため, 実際の細胞内では出会う事がないようなタンパク質間の相互作用もデータに含まれてしまう. この例のように生物データ一般に多くの擬陽性や疑陰性のあるデータが多数含まれている.

情報の散逸の応用～データに語らせないデータ解析

一般にデータにはノイズが含まれる. 特にデータが多かったり, 実験・計測方法が確立されていない, もしくは本質的に諸般の理由で観測・データを取得することが困難な場合, 本来であればとても使えないようなノイジーなデータを使わなくてはならない場合も多い. こうしたデータについて, そのまま解析をするととても信じられないような結果が出てくることは明白なので, 使うデータの数を減らしたり, 数理的な工夫をしたりするわけだが, そこで苦しむのは「なんとかデータを生かそう, データに語らせよう」とするためである.

高病原性インフルエンザウィルス（スペイン風邪）と, 鳥インフルエンザウィルスに感染させたサル（マカクサル）の遺伝子発現ビッグデータの例を示す. サルはインフルエンザウィルスに対して強く，鳥インフルエンザに感染させても, ウィルス性肺炎は発症するものの回復する. 一方で, スペイン風邪ウィルスに感染するとウィルス性肺炎を発症し, その病状は致死的なものとなる. そこで, サルが鳥インフルエンザに感染した場合と, スペイン風邪に感染した場合の肺での遺伝子発現を比較することで, 高病原性インフルエンザの致死的な病原性の機序を調査した．

実験データは, 一般的に使われているDNAマイクロアレイを用いて, 感染初期から20弱のタイムポイントで４万の遺伝子の遺伝子発現の時系列などを調査して得られたものである（それ以外のデータの解析も 並行して行った).

　　　　　　　　　　　　　　使用したDNAアレイデータの一部

ウィルス学やバイオインフォマティクス手法の詳細は省略するが, いわゆるDNAマイクロアレイ解析の手法で使えるものは全部使ってみたが, 生物学的に意味のある結果は得られなかった. この研究を行なった当時，ウィルス学では全遺伝子を網羅的に調査する研究はほとんど行われていなかった．

私たちは従来法と医薬研究用の商用のデータベースを用いて，全遺伝子発現の時系列をまとめて大きなマップを作成した．すると，本来は発現すべきウィルス応答の遺伝子群の時系列ネットワークがとても疎であったり，ある部分は他に比べて密になっていたりと，全体として情報の偏りがあるマップとなってしまった．

この研究を行なっているときに，関係していた国際プロジェクトの会議に参加する機会があった．その折に，プロジェクトの統括メンバーのある高名なウィルス学の研究者が，バイオインフォマティクスのチームの研究報告を途中で遮り

「そんな結果はすべて論文や教科書に書いてあることだ．そんな話を聞きたいんじゃない．今後は生物学者と話すな」

とコメントしていた．私たちが得た「予想外の結果」の理由をこのコメントが端的に示していた．私たちが使用していた高額な使用料がかかるウィルス学の商用データベースは，学位取得者が論文を読んで構築しているデータベースであり，まさに当時のウィルス学の主要な結果の集合体で，私たちはいわば「研究マップ」を作成していたことに気づかされた．

バイオインフォマティクスやシステム生物学は生物的な知見を用いて行うことが常道であるが「生物学者と話さずに」つまり数理的な方法のみを用いて生物データの分析を行うことの重要性を思い知らされた．そこで一般計算科学での成果の一つである, 先述した「情報の散逸」を用いることにした.

「情報の散逸」振動と安定

前回の課題では２つ目の「情報の散逸」の典型例を出題した．情報の散逸の典型例はLotoka VolterraやBZ反応のような「振動する系」である．

$X \xrightarrow{k_1} X,X$

$X,Y \xrightarrow{k_2} Y,Y$

$y \xrightarrow{k_3}$

一方で，前回に課題として出題した「情報の散逸」は，散逸項により系が安定化する例である．課題の微分方程式から素過程に書き下すと以下のようになる．

$X \xrightarrow{a} X,X,v$

$X,Y,v \xrightarrow{b} Y,Y$

$Y \xrightarrow{c}$

たとえば $X >> Y$の場合，散逸項$v$がなければ$Y$すぐに負になる．この系をLotoka Volterraと同様に生態系とすれば，$X,Y$は0もしくは正なので，種$Y$はただちに絶滅してしまう．だが，$v$が存在する場合，$b >> a$の場合は$Y$は絶滅を避けられる．

より具体的には，前回の課題でのLotoka Volterraの解析法（ヌルクライン法）をもちいて上述の数理モデルの平衡点を導き出すと，$\delta, \gamma$は定数であるので，$\frac{\delta}{\gamma v} \sim c\frac{1}{v},v>0$となる．つまり，LV系では2点であった平衡点が散逸項により無限に分岐する．

$\dot{X}=ax-bxyv=x(a-byv)$

$\dot{Y}=bxyv-cy=y(bxv-c)$

より平衡点集合は$y=\frac{a}{bv}, x=\frac{c}{bv}$となる．$y$が$c\frac{1}{v}$より大きいばあいは負，小さい場合は正となるため平衡点集合$\frac{c}{v}$に吸引され，$x$はその逆となりいずれにせよ平衡点集合$\frac{c}{v}$に吸引される．課題への解答で1名の方が指摘されていた通り，LVの平衡点のひとつは$v=1$の場合として含まれる．

高病原性インフルエンザによる致死的病原性の発現

情報の散逸には振動と安定の２種類の力学系があることを確認してきたが，では，対象にしていたインフルエンザの場合はどちらを用いるべきであろうか？私たちはヒトの肺の細胞（培養細胞）にインフルエンザウィルスを曝露する実験を行なった．そして，ウィルス の曝露量を低濃度から高濃度へと変えていった．基本的に遺伝子の発現は促進と抑制により振動している．だが，曝露量を濃くしていくことにより，それまでバラついていた発現ー抑制の様子が変化していく．だが，このパタンは「遺伝子の並べ方（縦軸）」に依存する．

そのため，私たちは

• 時系列パタンが類似し，かつ
• 生物学的機能が同じ

遺伝子をクラスタリングする方法を開発した．この方法でクラスタリングを行うと20,000程度の遺伝子を100程度のクラスタに分類することができる．

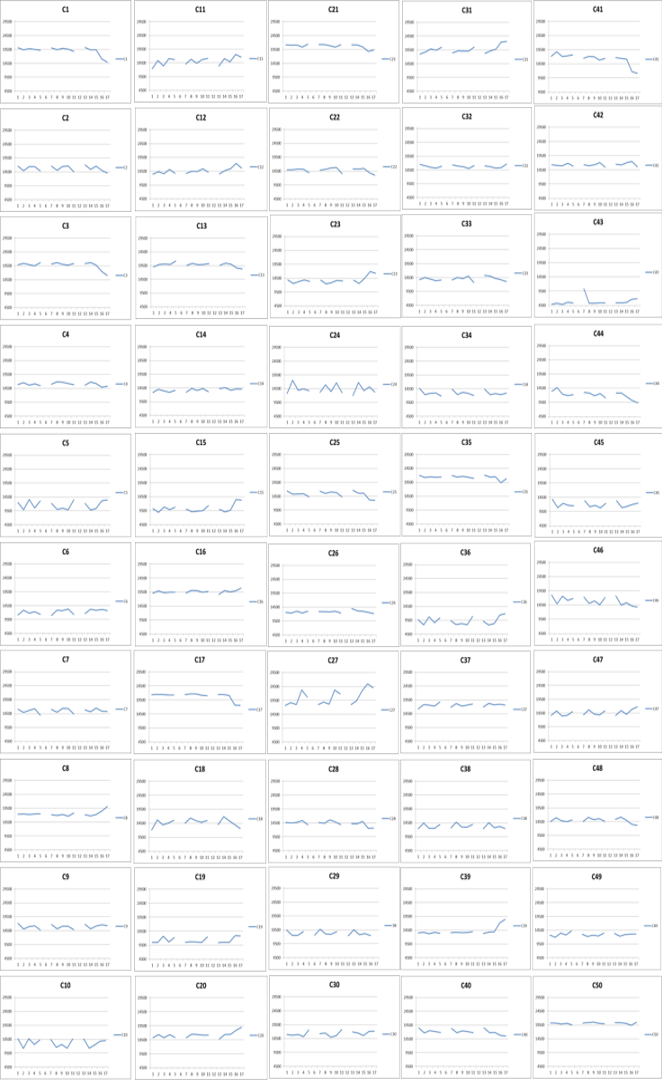
　　　　　　　　　　　　開発したクラスタリング法による遺伝子の分類

この分類にもとづき，遺伝子の配置を固定した上で，ウィルスを曝露する実験を行なった．

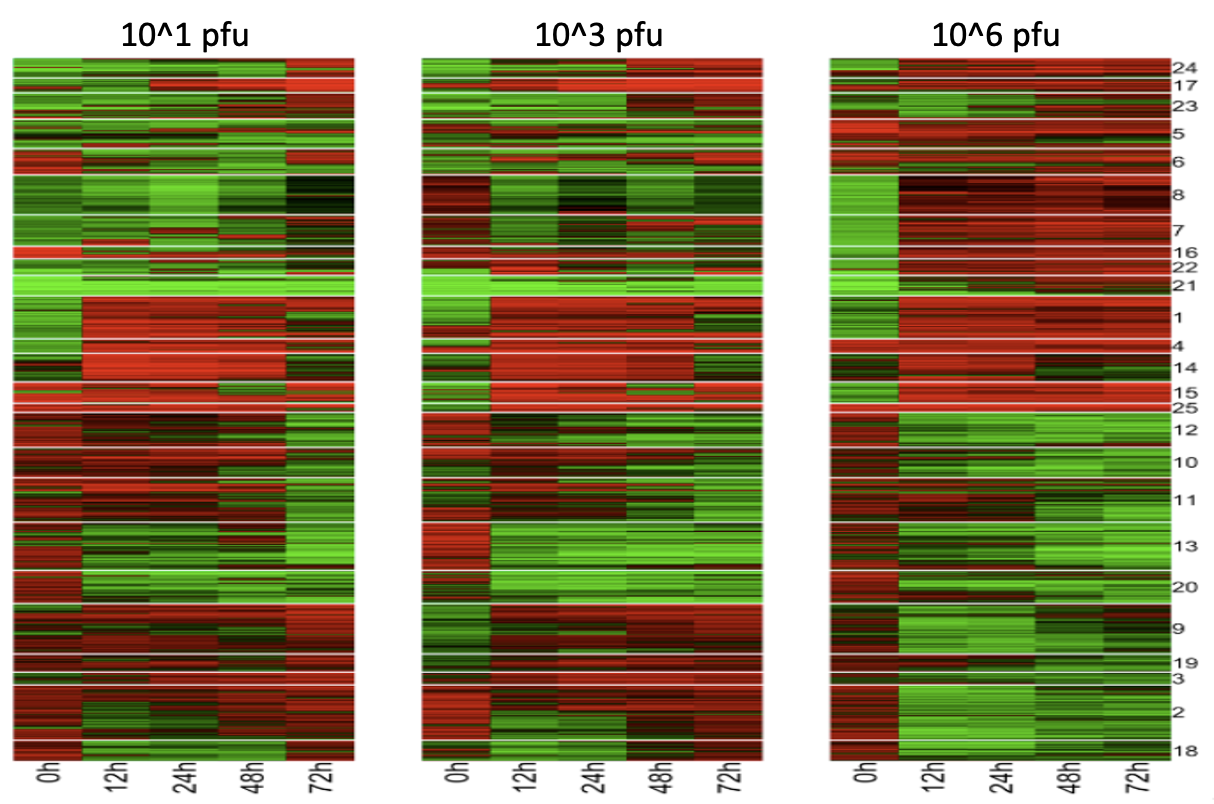
ウィルス 曝露実験（マイクロアレイ解析）．左から右に曝露量が濃くなっている．赤色が濃いほど発現量が多く，緑色が濃いほど抑制量が多い（コントロール値との相対値）．横軸は時間．

この実験から示唆されることは，曝露量が低濃度の場合には遺伝子は非同期的に振動しており，その振動パタンは生物学的機能に概ね依存していることである．興味ふかいのは，ウィルス の濃度が濃くなるに従って，それまでの発現ー抑制の振動が同期するようになり，さらには振動しなくなることである．

そこで，私たちの開発したクラスタリング法をもちいて分類した遺伝子群から相互に振動の促進と抑制を制御しているクラスタを抽出することで，系全体がどのように振動しているかを分析した．そして，この分析から，致死的病原性の発現につながる遺伝子群がみえてきた．

この分析では生物学的な知見は使わず，時系列解析と情報の散逸の概念のみから，結果を得ることができた．

課題：「情報の散逸」として解釈可能な自然現象（人工物を含む）の例をあげ，散逸項に相当するものを明示して説明しなさい．

今回はここまでです．おつかれさまでした．